【题目】(1)问题如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°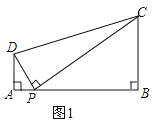
(1)求证:ADBC=APBP
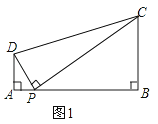
(2)探究如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A,设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切时,求t的值.
参考答案:
【答案】
(1)
解:如图1,
∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠ADP=∠BPC,
∴△ADP∽△BPC,
∴![]() =
=![]() ,
,
∴ADBC=APBP
(2)
解:
结论ADBC=APBP仍然成立.
理由:如图2,
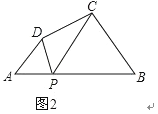
∵∠BPD=∠DPC+∠BPC,∠BPD=∠A+∠ADP,
∴∠DPC+∠BPC=∠A+∠ADP.
∵∠DPC=∠A=∠B=θ,
∴∠BPC=∠ADP,
∴△ADP∽△BPC,
∴![]() =
=![]() ,
,
∴ADBC=APBP
(3)
解:如图3,
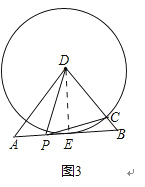
过点D作DE⊥AB于点E.
∵AD=BD=5,AB=6,
∴AE=BE=3.
由勾股定理可得DE=4.
∵以点D为圆心,DC为半径的圆与AB相切,
∴DC=DE=4,
∴BC=5﹣4=1.
又∵AD=BD,
∴∠A=∠B,
∴∠DPC=∠A=∠B.
由(1)、(2)的经验可知ADBC=APBP,
∴5×1=t(6﹣t),
解得:t1=1,t2=5,
∴t的值为1秒或5秒.
【解析】(1)如图1,由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证得△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(2)如图2,由∠DPC=∠A=∠B=θ可得∠ADP=∠BPC,即可证得△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(3)如图3,过点D作DE⊥AB于点E,根据等腰三角形的性质可得AE=BE=3,根据勾股定理可得DE=4,由题可得DC=DE=4,则有BC=5﹣4=1.易证∠DPC=∠A=∠B.根据ADBC=APBP,就可求出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 甲、乙两名车工都加工要求尺寸是直径10毫米的零件.从他们所生产的零件中,各取5件,测得直径如下(单位:毫米)
甲:10.05, 10.02,9.97,9.95,10.01
乙:9.99,10.02,10.02,9.98,10.01
分别计算两组数据的标准差(精确到0.01),说明在尺寸符合规格方面,谁做得较好?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6名,7名,8名,10名,12名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.
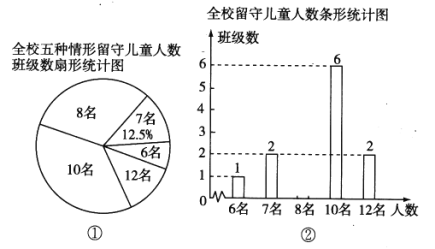
请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图.
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥AD,交射线AD于点M.

(1)当点E在边BC上,点M在边AD的延长线上时,如图①,求证:AB+BE=AM;
(提示:延长MF,交边BC的延长线于点H.)
(2)当点E在边CB的延长线上,点M在边AD上时,如图②;当点E在边BC的延长线上,点M在边AD上时,如图③.请分别写出线段AB,BE,AM之间的数量关系,不需要证明;
(3)在(1),(2)的条件下,若BE= ,∠AFM=15°,则AM=.
,∠AFM=15°,则AM=. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.
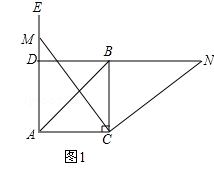
(1)直接写出∠NDE的度数.
(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由.

(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD= ,其他条件不变,求线段AM的长.
,其他条件不变,求线段AM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
在一个三角形中,各边和它所对角的正弦的比相等, =
= =
= ,利用上述结论可以求解如下题目:
,利用上述结论可以求解如下题目:
在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.
解:在△ABC中,∵ =
= ∴b=
∴b= =
= =
= =3
=3 .
.
理解应用:
如图,甲船以每小时30 海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10 海里.
海里.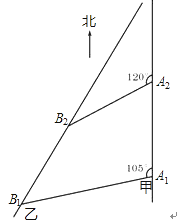
(1)判断△A1A2B2的形状,并给出证明
(2)求乙船每小时航行多少海里? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE

(1)请判断:AF与BE的数量关系是 , 位置关系是 .
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
相关试题

