【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC.
(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.

参考答案:
【答案】(1)∠C=32°;(2)45°.
【解析】试题分析:连接OB,根据切线的性质,得∠OBA=90°,又∠A=26°,所以∠AOB=64°,再用三角形的外角性质可以求出∠ACB的度数.
(2)由角平分线及三角形外角性质可得∠C+∠CAE=∠FBA+∠BAF,即∠BEF=∠BFE,再利用直径所对的圆周角是直角即可求解.
试题解析:(1)如图:连接OB,
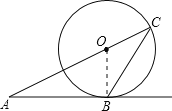
∵AB切⊙O于点B,
∴∠OBA=90°,
∵∠A=26°,
∴∠AOB=90°-26°=64°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC=2∠ACB,
∴∠ACB=32°.
(2)如图,连接BD交AE于点F.
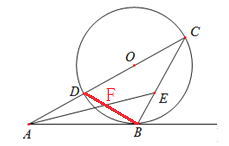
∵AB是⊙O的切线,
∴∠C=∠DBA.
又∵AE是∠CAB的平分线,
∴∠CAE=∠BAE,
∴∠C+∠CAE=∠ABD+∠BAE,
∴∠AEB=∠BFE.
∵CD是⊙O直径,
∴∠CBD=90°.
∴∠AEB=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用简便方法计算:1.42×16-2.22×4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动.已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).

(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由. -
科目: 来源: 题型:
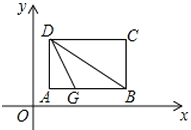
查看答案和解析>>【题目】如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
(1)求AG的长;
(2)在坐标平面内存在点M(m,-1)使AM+CM最小,求出这个最小值;
(3)求线段GH所在直线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥DE,∠ABC=70,∠CDE=140,则∠BCD的值为( )
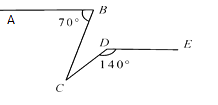
A.70
B.50
C.40
D.30 -
科目: 来源: 题型:
查看答案和解析>>【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 ;

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知太阳的半径约为696000000m,696000000这个数用科学记数法表示为
相关试题

