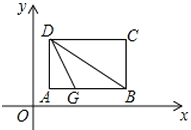
【题目】如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
(1)求AG的长;
(2)在坐标平面内存在点M(m,-1)使AM+CM最小,求出这个最小值;
(3)求线段GH所在直线的解析式.
参考答案:
【答案】(1)AG=1.5;AM+CM最小值为![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据折叠的性质可得AG=GH,设AG的长度为x,在Rt△HGB中,利用勾股定理求出x的值;
(2)作点A关于直线y=-1的对称点A',连接CA'与y=-1交于一点,这个就是所求的点,求出此时AM+CM的值;
(3)求出G、H的坐标,然后设出解析式,代入求解即可得出解析式.
试题解析:(1)由折叠的性质可得,AG=GH,AD=DH,GH⊥BD,
∵AB=4,BC=3,
∴BD=![]() ,
,
设AG的长度为x,
∴BG=4-x,HB=5-3=2,
在Rt△BHG中,GH2+HB2=BG2,
x2+4=(4-x)2,
解得:x=1.5,
即AG的长度为1.5;
(2)如图所示:作点A关于直线y=-1的对称点A',连接CA'与y=-1交于M点,
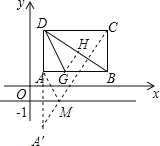
∵点B(5,1),
∴A(1,1),C(5,4),A'(1,-3),
AM+CM=A'C=![]() ,
,
即AM+CM的最小值为![]() ;
;
(3)∵点A(1,1),
∴G(2.5,1),
过点H作HE⊥AD于点E,HF⊥AB于点F,如图所示,
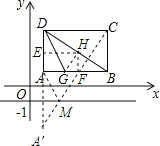
∴△AEH∽△DAB,△HFB∽△DAB,
∴![]() ,
, ![]() ,
,
即![]() ,
, ![]() ,
,
解得:EH=![]() ,HF=
,HF=![]() ,
,
则点H(![]() ,
, ![]() ),
),
设GH所在直线的解析式为y=kx+b,
则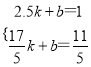 ,解得:
,解得: 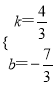 ,
,
则解析式为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的主视图、左视图、俯视图都是长方形,这个几何体可能是( )
A. 长方体B. 四棱锥C. 三棱锥D. 圆锥
-
科目: 来源: 题型:
查看答案和解析>>【题目】用简便方法计算:1.42×16-2.22×4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动.已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).

(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC.
(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥DE,∠ABC=70,∠CDE=140,则∠BCD的值为( )
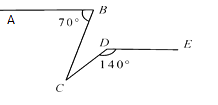
A.70
B.50
C.40
D.30 -
科目: 来源: 题型:
查看答案和解析>>【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 ;

相关试题

