【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
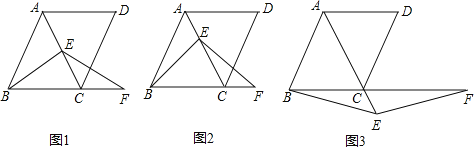
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
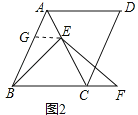
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
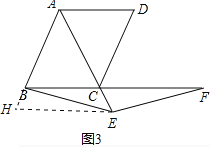
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
参考答案:
【答案】(1)△ABC的面积=![]() ;(2)见解析;(3)成立,证明见解析.
;(2)见解析;(3)成立,证明见解析.
【解析】
试题分析:(1)根据菱形的性质证明△ABC是等边三角形和AB=2,求出△ABC的面积;
(2)作EG∥BC交AB于G,证明△BGE≌△ECF,得到BE=EF;
(3)作EH∥BC交AB的延长线于H,证明△BHE≌△ECF,得到BE=EF.
解:(1)∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,又E是线段AC的中点,
∴BE⊥AC,AE=![]() AB=1,
AB=1,
∴BE=![]() ,
,
∴△ABC的面积=![]() ×AC×BE=
×AC×BE=![]() ;
;
(2)如图2,作EG∥BC交AB于G,
∵△ABC是等边三角形,
∴△AGE是等边三角形,
∴BG=CE,
∵EG∥BC,∠ABC=60°,
∴∠BGE=120°,
∵∠ACB=60°,
∴∠ECF=120°,
∴∠BGE=∠ECF,
在△BGE和△ECF中,
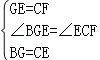 ,
,
∴△BGE≌△ECF,
∴EB=EF;
(3)成立,
如图3,作EH∥BC交AB的延长线于H,
∵△ABC是等边三角形,
∴△AHE是等边三角形,
∴BH=CE,
在△BHE和△ECF中,
 ,
,
∴△BHE≌△ECF,
∴EB=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=
 (x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.
(x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.
(1)求△OCD的面积;
(2)当BE=
 AC时,求CE的长.
AC时,求CE的长. -
科目: 来源: 题型:
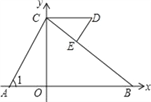
查看答案和解析>>【题目】如图,平面直角坐标系中,C(0,5)、D(a,5)(a>0),A、B在x轴上,∠1=∠D,请写出∠ACB和∠BED数量关系以及证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各图中的MA1与NAn平行.
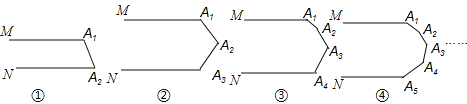
(1)图①中的∠A1+∠A2= 度,图②中的∠A1+∠A2+∠A3= 度,
图③中的∠A1+∠A2+∠A3+∠A4= 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度,…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10= 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(m﹣1)x2+5x+m2﹣3m+2=0有一个根为0,则m的值( )
A.0
B.1或2
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两班分别由10名选手参加健美比赛,两班参赛选手身高的方差分别是S甲2=1.5,S乙2=2.5,则下列说法正确的是( )
A.甲班选手比乙班选手的身高整齐
B.乙班选手比甲班选手的身高整齐
C.甲、乙两班选手的身高一样整齐
D.无法确定哪班选手的身高整齐 -
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段为边,能组成三角形的是( )
A. 2cm,5 cm,8cm B. 3 cm,3 cm,6 cm
C. 3 cm,4 cm,5 cm D. 1 cm,2cm,3 cm
相关试题

