【题目】如图,在平行四边形ABCD中,
(1)以点A为圆心,AB长为半径画弧交AD于点F,再分别以B、F为圆心,大于 ![]() BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF;
BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF;
(2)四边形ABEF是(选填矩形、菱形、正方形、无法确定),说明理由.
参考答案:
【答案】
(1)
解:如图所示;
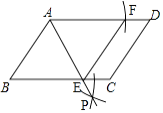
(2)菱形
【解析】菱形,理由如下:
∵在平行四边形ABCD中,AF∥BC,
∴∠FAE=∠AEB,
由(1)知∠BAE=∠FAE,
∴∠BAE=∠AEB,
∴AB=BE,
∵AB=AF,
∴BE=AF,
∴四边形ABEF是菱形,
所以答案是:菱形.
(1)根据要求作图即可;(2)由(1)作图知∠BAE=∠FAE,结合∠FAE=∠AEB得∠BAE=∠AEB,从而得AB=BE,进一步由菱形的判定可得.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图所示的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3 , …分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是 .
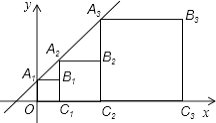
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空,完成下列说理过程
如图,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数
解:因为∠AOB=90°.
所以∠BOC+∠AOC=90°
因为∠COD=90°
所以∠AOD+∠AOC=90°.
所以∠BOC=∠AOD. ( )
因为∠BOC=20°.
所以∠AOD=20°.
因为OA平分∠DOE
所以∠ =2∠AOD= °. ( )
所以∠COE=∠COD﹣∠DOE= °

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
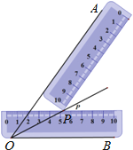
A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 三角形三条垂直平分线的交点到三个定点的距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】有A、B两种饮料,这两种饮料的体积和单价如表:
类型
A
B
单瓶饮料体积/升
1
2.5
单价/元
3
4
(1)小明购买A、B两种饮料共13升,用了25元,他购买A,B两种饮料个各多少瓶?
(2)若购买A、B两种饮料共36瓶,且A种饮料的数量不多于B种饮料的数量,则最少可以购买多少升饮料?
相关试题

