【题目】数学思考: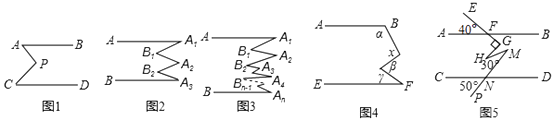
(1)如图1,已知AB∥CD,探究下面图形中∠APC和∠PAB、∠PCD的关系,并证明你的结论
(2)①如图2,已知AA1∥BA1 , 请你猜想∠A1 , ∠B1 , ∠B2 , ∠A2、∠A3的关系,并证明你的猜想;
②如图3,已知AA1∥BAn , 直接写出∠A1 , ∠B1 , ∠B2 , ∠A2、…∠Bn﹣1、∠An的关系
(3)①如图4所示,若AB∥EF,用含α,β,γ的式子表示x,应为
A.180°+α+β﹣γ B.180°﹣α﹣γ+β C.β+γ﹣α D.α+β+γ
②如图5,AB∥CD,且∠AFE=40°,∠FGH=90°,∠HMN=30°,∠CNP=50°,请你根据上述结论直接写出∠GHM的度数是 .
参考答案:
【答案】
(1)证明:如图1,过点P作OP∥AB,
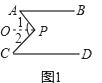
∵AB∥CD,
∴OP∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∴∠APC=∠1+∠2=∠PAB+∠PCD,
即∠APC=∠PAB+∠PCD
(2)解:①如图2,过点A2作A2O∥AA1,
由(1)可知∠B1=∠A1+∠1,∠B2=∠2+∠A3,
所以,∠B1+∠B2=∠A1+∠A2+∠A3;
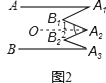
②如图3,由①可知:
∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn﹣1
(3)B,30°
【解析】解:(1)如图1,过点P作OP∥AB,
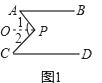
∵AB∥CD,
∴OP∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∴∠APC=∠1+∠2=∠PAB+∠PCD,
即∠APC=∠PAB+∠PCD
(2)①如图2,过点A2作A2O∥AA1,
由(1)可知∠B1=∠A1+∠1,∠B2=∠2+∠A3,
所以,∠B1+∠B2=∠A1+∠A2+∠A3;

②如图3,由①可知:
∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn﹣1
(3)①如图4,过∠x的顶点作CD∥AB,
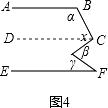
则∠x=(180°﹣α)+(β﹣γ)=180°﹣α﹣γ+β,
②如图5,由(1)可知,40°+∠GHM+50°=∠G+∠M,
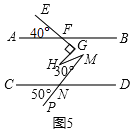
∵∠G=90°,∠M=30°,
∴∠GHM=90°+30°﹣40°﹣50°=30°.
所以答案是:(1)∠APC=∠PAB+∠PCD;(2)∠B1+∠B2=∠A1+∠A2+∠A3;∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn﹣1;(3)B;30°.
【考点精析】通过灵活运用平行线的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是一元二次方程x2﹣2mx+1=0的一个解,则m的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1 , y1)平移后的对应点为P′(x1+6,y1+4).
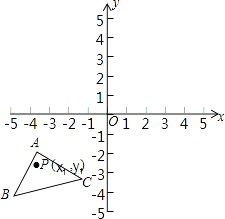
(1)请在图中作出△A′B′C′;
(2)写出点A′、B′、C′的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠A=60°,AB=4
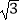 ,点P在对角线AC上,且PB=PD=4,则∠PDC的度数为 .
,点P在对角线AC上,且PB=PD=4,则∠PDC的度数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
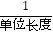
(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形.请列举出所有满足条件的三角形.
(2)用直尺和圆规作出三边满足a<b<c的三角形(用给定的单位长度,不写作法,保留作图痕迹). -
科目: 来源: 题型:
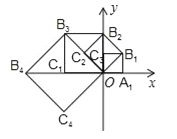
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是 .
-
科目: 来源: 题型:
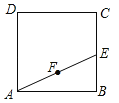
查看答案和解析>>【题目】如图,正方形ABCD的面积为3cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.
相关试题

