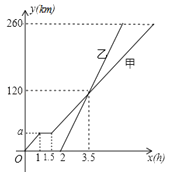
【题目】甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)求出图中a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函数表达式,并写出相应的x的取值范围;
(3)当甲车行驶多长时间时,两车恰好相距40km.
参考答案:
【答案】(1)40;(2)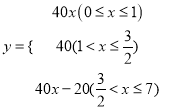 ;(3)行驶1小时或(1-1.5)小时或2.5小时或4.5小时,两车恰好相距40km.
;(3)行驶1小时或(1-1.5)小时或2.5小时或4.5小时,两车恰好相距40km.
【解析】试题分析:(1)求出甲的速度,根据休息前后速度相同和距离等于速度乘时间求出a的值;
(2)根据图象中自变量的取值范围分别求出各段的函数表达式;
(3)分别从甲在乙前和甲在乙后两种情况列出方程,求出时间.
试题解析:解:(1)由题意120÷(3.5﹣0.5)=40,a=1×40=40;
(2)①当0≤x≤1时,设y与x之间的函数关系式为y=k1x,把(1,40)代入,得k1=40
∴y=40x;
②当1<x≤![]() 时,y=40;
时,y=40;
③当![]() <x≤7时,设y与x之间的函数关系式为y=k2x+b,由题意,得:
<x≤7时,设y与x之间的函数关系式为y=k2x+b,由题意,得: 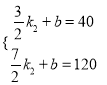 ,解得:
,解得: ![]() ,∴y=40x﹣20;
,∴y=40x﹣20;
综上所述: 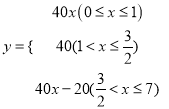 ;
;
(3)设乙车行驶的路程y与时间x之间的解析式为y=mx+n,由题意,得: 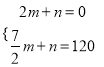 ,解得:
,解得: ![]() ,∴y=80x﹣160,当40x﹣20﹣(80x﹣160)=40时,解得:x=2.5.
,∴y=80x﹣160,当40x﹣20﹣(80x﹣160)=40时,解得:x=2.5.
当80x﹣160﹣(40x﹣20)=40时,解得:x=4.5.
答:甲车行驶1小时(或1﹣1.5小时)或2.5小时或4.5小时,两车恰好相距40km.
-
科目: 来源: 题型:
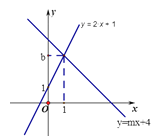
查看答案和解析>>【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】张老师计划到超市购买甲种文具100个,他到超市后发现还有乙种文具可供选择,如果调整文具的购买品种,每减少购买1个甲种文具,需增加购买2个乙种文具.设购买x个甲种文具时,需购买y个乙种文具.
(1)①当减少购买1个甲种文具时,x=______,y=________;
②求y与x之间的函数表达式.
(2)已知甲种文具每个5元,乙种文具每个3元,张老师购买这两种文具共用去540元,甲、乙两种文具各购买了多少个?
-
科目: 来源: 题型:
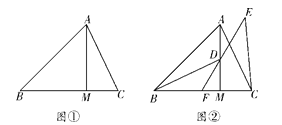
查看答案和解析>>【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图①,若AB=3
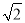 ,BC=5,求AC的长;
,BC=5,求AC的长;(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1) 令P0(2,-3),O为坐标原点,则d(O,P0)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离. 若P(a,-3)到直线y=x+1的直角距离为6,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.
(1)求证:BM=AC;
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年夏季,湖南省部分地区发生了罕见的旱灾,连续几个月无有效降水.为抗旱救灾,驻湘某部计划为驻地村民新建水渠3600米,为使水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.求实际每天修水渠多少米?(列方程解答)
相关试题

