搜索
【题目】张老师计划到超市购买甲种文具100个，他到超市后发现还有乙种文具可供选择，如果调整文具的购买品种，每减少购买1个甲种文具，需增加购买2个乙种文具．设购买x个甲种文具时，需购买y个乙种文具．
(1)①当减少购买1个甲种文具时，x＝______，y＝________；
②求y与x之间的函数表达式．
(2)已知甲种文具每个5元，乙种文具每个3元，张老师购买这两种文具共用去540元，甲、乙两种文具各购买了多少个？
参考答案：
【答案】（1）y=-2x+100；（2）甲乙两种文具各购买了60个和80个.
【解析】试题分析：（1）①根据“每减少购买1个甲种文具，需增加购买2个乙种文具”可直接求解；
②根据①的结论直接列式即可求出函数的解析式；
（2）根据题意列出二元一次方程组求解即可.
试题解析：（1）①99，2.
②根据题意，得
.
所以
与
之间的函数表达式为
.
（2）根据题意，得
解得
答：甲、乙两种文具各购买了60个和80个.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是由边长为1个单位长度的小正方形组成的网格图．
（1）请在图中建立平面直角坐标系，使A、B两点的坐标分别为A（2，3）、B（-2，0）；
（2）正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形，在图中画出格点△ABC使得AB=AC，请写出在（1）中所建坐标系内所有满足条件的点C的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD⊥BC于D，BD=AD，DG=DC，E，F分别是BG，AC的中点．
（1）求证：DE=DF，DE⊥DF；
（2）连接EF，若AC=10，求EF的长．
-
科目： 来源： 题型：
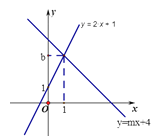
查看答案和解析>>【题目】如图，直线l1：y=2x+1与直线l2：y=mx+4相交于点P（1，b）
(1)求b，m的值
(2)垂直于x轴的直线x=a与直线l1，l2分别相交于C，D，若线段CD长为2，求a的值
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠ABM＝45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC.
(1)如图①，若AB＝3
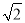,BC＝5，求AC的长；(2)如图②，点D是线段AM上一点，MD＝MC，点E是△ABC外一点，EC＝AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF＝∠CEF.
-
科目： 来源： 题型：
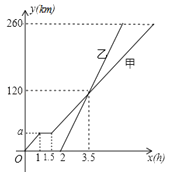
查看答案和解析>>【题目】甲、乙两车从A地驶向B地，甲车比乙车早行驶2h，并且在途中休息了0.5h，休息前后速度相同，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．
（1）求出图中a的值；
（2）求出甲车行驶路程y（km）与时间x（h）的函数表达式，并写出相应的x的取值范围；
（3）当甲车行驶多长时间时，两车恰好相距40km．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于平面直角坐标系中的任意两点P1(x1,y1)，P2(x2,y2)，我们把|x1－x2|+|y1－y2|叫做P1、P2两点间的直角距离，记作d(P1,P2)．
(1) 令P0(2,－3)，O为坐标原点，则d(O,P0)＝ ；
(2)已知O为坐标原点，动点P(x,y)满足d(O,P)＝1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形；
(3)设P0(x0,y0)是一定点，Q(x,y)是直线y=ax+b上的动点，我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离． 若P(a,－3)到直线y=x＋1的直角距离为6，求a的值．
相关试题
