【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
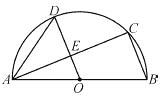
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
参考答案:
【答案】(1)35°;(2)![]() .
.
【解析】试题分析:根据OD∥BC,∠DOA=∠B=70°,根据OA=OD可得∠DAO=∠ADO=55°,根据AB为直径可求出∠CAD的度数;根据Rt△ACB得出BC的长度,根据O为AB的中点,OD∥BC,从而得出OE和OD的长度,根据DE=OD-OE得出答案.
试题解析:(1)∵OD∥BC,∴∠DOA=∠B=70°. 又∵OA=OD,∴∠DAO=∠ADO=55°.
∵AB是直径,∴∠ACB=90°,∴∠CAB=20° ∴∠CAD=35°.
(2)在Rt△ACB中,BC=![]() . ∵圆心O是直径AB的中点,OD∥BC,
. ∵圆心O是直径AB的中点,OD∥BC,
∴OE=![]() BC=
BC=![]() 又OD=
又OD=![]() AB=2, ∴DE=OD-OE=2-
AB=2, ∴DE=OD-OE=2-![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】资料:小球沿直线撞击水平格档反弹时(不考虑垂直撞击),撞击路线与水平格档所成的锐角等于反弹路线与水平格档所成的锐角.以图(1)为例,如果黑球
 沿从
沿从  到
到  方向在
方向在  点处撞击
点处撞击  边后将沿从
边后将沿从  到
到  方向反弹,根据反弹原则可知
方向反弹,根据反弹原则可知  ,即
,即  .如图(2)和(3),
.如图(2)和(3), 是一个长方形的弹子球台面,有黑白两球
是一个长方形的弹子球台面,有黑白两球  和
和  ,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)
,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)
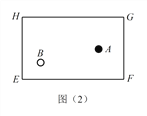

(1)探究(1):黑球
 沿直线撞击台边
沿直线撞击台边  哪一点时,可以使黑球
哪一点时,可以使黑球  经台边
经台边  反弹一次后撞击到白球
反弹一次后撞击到白球  ?请在图(2)中画出黑球
?请在图(2)中画出黑球  的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.
的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.(2)探究(2):黑球
 沿直线撞击台边
沿直线撞击台边  哪一点时,可以使黑球
哪一点时,可以使黑球 
先撞击台边  反弹一次后,再撞击台边
反弹一次后,再撞击台边 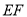 反弹一次撞击到白球
反弹一次撞击到白球  ?请在图(3)中画出黑球
?请在图(3)中画出黑球 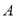 的路线图,标出黑球撞击
的路线图,标出黑球撞击  边的撞击点,简单说明作法,不用证明.
边的撞击点,简单说明作法,不用证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知5a+2的立方根是3,3a+b-1的算术平方根是4,求a+2b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4x2+mxy+9y2是一个完全平方式,则m=( )
A.6B.12C.±6D.±12
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词.根据调查结果,该小组绘制了如下的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学?
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,热词B所在扇形的圆心角是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线l∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=90°,直线AQ交y轴于点C.
(1)当a=
 时,求点Q的坐标;
时,求点Q的坐标;(2)当PA+PO最小时,求a.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y=
 (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式.

相关试题

