【题目】如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: ①△AED≌△DFB;②S四边形BCDG= ![]() CG2;③若AF=2DF,则BG=6GF.
CG2;③若AF=2DF,则BG=6GF.
其中正确的结论( )
A.只有①②
B.只有①③
C.只有②③
D.①②③
参考答案:
【答案】D
【解析】解:①∵ABCD为菱形,∴AB=AD. ∵AB=BD,∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB;
②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.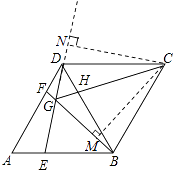
∴CM=CN,
∵ ![]() ,
,
∴△CBM≌△CDN,(HL)
∴S四边形BCDG=S四边形CMGN .
S四边形CMGN=2S△CMG ,
∵∠CGM=60°,
∴GM= ![]() CG,CM=
CG,CM= ![]() CG,
CG,
∴S四边形CMGN=2S△CMG=2× ![]() ×
× ![]() CG×
CG× ![]() CG=
CG= ![]() CG2 .
CG2 .
③过点F作FP∥AE于P点.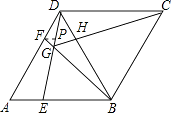
∵AF=2FD,
∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=1:6=FG:BG,
即 BG=6GF.
故选D.
【考点精析】解答此题的关键在于理解平行线分线段成比例的相关知识,掌握三条平行线截两条直线,所得的对应线段成比例,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为 ,B4的坐标为 .
(2)按以上规律将△OAB进行n次变换得到△OAnBn,则An的坐标为 ,Bn的坐标为 ;
(3)△OAnBn的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+
x2+  x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.
x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.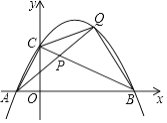
(1)①写出点A,B,C的坐标:A(),B(),C();
②求证:△ABC是直角三角形;
(2)记△BCQ的面积为S,求S关于x的函数表达式;
(3)在点P的运动过程中,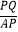 是否存在最大值?若存在,求出
是否存在最大值?若存在,求出 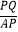 的最大值及点Q的坐标;若不存在,请说明理由.
的最大值及点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣18×(﹣2)÷3
(2)(﹣
 )×(﹣90)÷
)×(﹣90)÷
(3)﹣2.5÷
 ×(﹣
×(﹣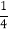 );
);(4)(﹣10)2﹣[16+(﹣3)2]
(5)(
 ﹣
﹣ +2)÷
+2)÷
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了二次根式的相关运算后,我们发现一些含有根号的式子可以表示成另一个式子的平方,如:
3+2
 =2+2
=2+2 +1=(
+1=( )2+2
)2+2 +1=(
+1=( +1)2;
+1)2;5+2
 =2+2
=2+2 +3=(
+3=( )2+2×
)2+2× ×
× +(
+( )2=(
)2=( +
+ )2
)2(1)请仿照上面式子的变化过程,把下列各式化成另一个式子的平方的形式:
①4+2
 ;②6+4
;②6+4
(2)若a+4
 =(m+n
=(m+n )2,且a,m,n都是正整数,试求a的值.
)2,且a,m,n都是正整数,试求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC﹣CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.

(1)当2<m≤8时,AP=,AQ=.(用m的代数式表示)
(2)当线段FG长度达到最大时,求m的值;
(3)在点P,Q整个运动过程中, ①当m为何值时,⊙O与△ABC的一边相切?
②直接写出点F所经过的路径长是.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】填在如图各正方形中的四个数之间都有相同的规律,根据这种规律,m的值是 .

相关试题

