【题目】如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,求∠BOE的度数. 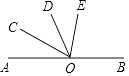
参考答案:
【答案】解:设∠DOE=x,则∠BOE=2x, ∵∠BOD=∠BOE+∠EOD
∴∠BOD=3x
∴∠AOD=180°﹣∠BOD=180°﹣3x
∵OC平分∠AOD
∴∠COD= ![]() ∠AOD=90°﹣
∠AOD=90°﹣ ![]() x
x
∵∠COE=∠COD+∠DOE=90°﹣ ![]() x+x=90°﹣
x+x=90°﹣ ![]()
∴90°﹣ ![]() =α
=α
∴x=180°﹣2α,即∠DOE=180°﹣2α
∴∠BOE=360°﹣4α
【解析】设∠DOE=x,则∠BOE=2x,用含x求出∠COE的表达式,然后根据∠COE=α列出方程即可求出∠BOE的度数.
【考点精析】利用角的平分线和角的运算对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】找规律.
一张长方形桌子可坐6人,按如图方式把桌子拼在一起.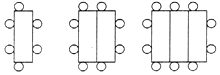
(1)2张桌子拼在一起可坐人;
3张桌子拼在一起可坐人;
n张桌子拼在一起可坐人.
(2)一家餐厅有45张这样的长方形桌子,按照如图方式每5张桌子拼成一张大桌子,请问45张长方形桌子这样摆放一共可坐多少人. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=15,AC=13,高AD=12,则△ABC的面积为______________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班学生在希望工程献爱心的捐献活动中,将省下的零用钱为贫困山区失学儿童捐款,有15位同学捐了20元,20位同学捐了10元,3位同学捐了8元,10位同学捐了5元捐了,2位同学捐了3元,则该班学生共捐款___________元,平均捐款__________元,其中众数是_____________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.
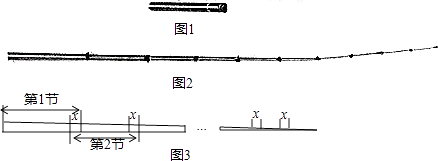
(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形的每个内角度数为( )
A.60°B.120°C.135°D.150°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A,B分别表示数a,3,点A关于原点O的对称点为点C.如果C为AB的中点,那么a的值为( )
A.﹣3B.﹣1C.1D.3
相关试题

