【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.得平行四边形ABDC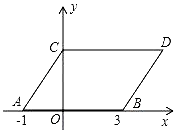
(1)直接写出点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC , 求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
请画出图形,直接写出∠CPO、∠DCP、∠BOP的数量关系.
参考答案:
【答案】
(1)
解:(1)∵将A(﹣1,0),B(3,0)分别向上平移2个单位,再向右平移1个单位,
∴C(0,2),D(4,2)
(2)
∵AB=4,CO=2,
∴S平行四边形ABDC=ABCO=4×2=8,
设M坐标为(0,m),
∴ ![]() ×4×|m|=8,解得m=±4
×4×|m|=8,解得m=±4
∴M点的坐标为(0,4)或(0,﹣4)
(3)
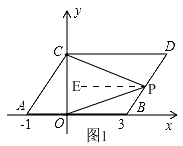
①当点P在BD上,如图1,
由平移的性质得,AB∥CD,
过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
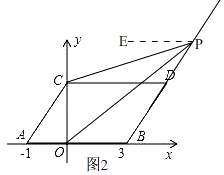
②当点P在线段BD的延长线上时,如图2,
由平移的性质得,AB∥CD,
过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠OPE﹣∠CPE=∠BOP﹣∠DCP,
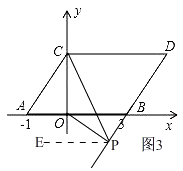
③当点P在线段DB的延长线上时,如图3,
同(2)的方法得出∠CPO=∠DCP﹣∠BOP.
【解析】(1)根据向上平移纵坐标加,向右平移横坐标加求出点C、D的坐标即可,(2)利用平行四边形的面积公式和三角形的面积公式列式计算即可得;(3)分三种情况,根据平移的性质可得AB∥CD,再过点P作PE∥AB,根据平行公理可得PE∥CD,然后根据两直线平行,内错角相等可得∠DCP=∠CPE,∠BOP=∠OPE即可得出结论.
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直角三角形中的两个锐角之差为22°,则较小的一个锐角的度数是( )
A.24°
B.34°
C.44°
D.46° -
科目: 来源: 题型:
查看答案和解析>>【题目】假期顾老师带学生乘车外出旅游,在乘车单价相同的情况下,甲、乙两位车主给出了不同的优惠方案.甲车主说“每人八折”,乙车主说“学生九折,老师免费”.李老师计算了一下,无论坐谁的车,费用都一样,则李老师带的学生为 ( )
A. 10名 B. 9名 C. 8名 D. 17名
-
科目: 来源: 题型:
查看答案和解析>>【题目】当a≤x≤a+1时,函数y=x2﹣2x+1的最小值为1,则a的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一元二次方程(1+x)(x+3)=2x2+1化成一般形式是:__________________;它的二次项系数是_________;一次项系数是________。
-
科目: 来源: 题型:
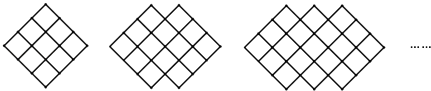
查看答案和解析>>【题目】下列图形都是由边长为“1”的小正方形按一定规律组成,其中第1个图形有9个边长为1的小正方形,第2个图形有14个边长为1的小正方形…则第10个图形中边长为1的小正方形的个数为( )
A.72
B.64
C.54
D.50 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数
 (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
相关试题

