【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20 800元,若两校联合组团只需花费18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
(2)两所学校报名参加旅游的学生各有多少人?
参考答案:
【答案】
(1)解:这两所学校报名参加旅游的学生人数之和超过200人,理由为:
设两校人数之和为a,
若a>200,则a=18000÷75=240;
若100<a≤200,则a=18000÷85=211 ![]() >200,不合题意,
>200,不合题意,
则这两所学校报名参加旅游的学生人数之和等于240人,超过200人
(2)解:设甲学校报名参加旅游的学生有x人,乙学校报名参加旅游的学生有y人,则
①当100<x≤200时,得 ![]()
解得 ![]() (6分)
(6分)
②当x>200时,得 ![]()
解得 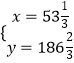 不合题意,舍去.
不合题意,舍去.
答:甲学校报名参加旅游的学生有160人,乙学校报名参加旅游的学生有80人
【解析】
①由已知分两种情况讨论而得出结论.
②根据两种情况的费用分别设未知数列出方程组求解,讨论出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,三角形ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2),现将三角形ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
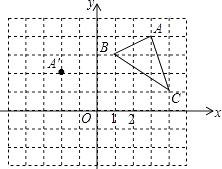
(1)请画出平移后的三角形A′B′C′(不写画法),并写出点B′、C′的坐标;
(2)求三角形ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF

(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
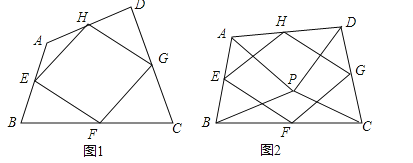
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.
求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式3x﹣m≥5的解集如图所示,则m的值等于( )
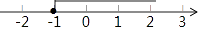
A.
B.﹣1
C.﹣5
D.﹣8 -
科目: 来源: 题型:
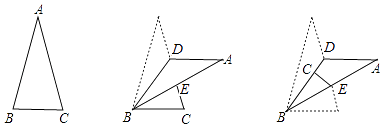
查看答案和解析>>【题目】在△ABC中,∠A=30°,D是AC边上的点;先将△ABC沿着BD翻折,翻折后△ABD的边AB交AC于点E;又将△BCE沿着BE翻折,C点恰好落在BD上,此时∠BEC=78°,则原三角形的∠ABC=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角三角形ABC中(AB>AC),AH⊥BC,垂足为H,E、D、F分别是各边的中点,则四边形EDHF是( )

A.梯形
B.等腰梯形
C.直角梯形
D.矩形
相关试题

