【题目】如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断∠AED与∠ACB的大小关系,并说明你的理由.
(2)若D、E、F分别是AB、AC、CD边上的中点,S四边形ADFE=4(平方单位),求S△ABC . 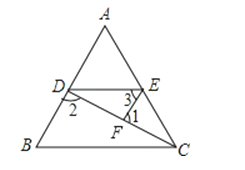
参考答案:
【答案】解:(1)相等.
∵∠1+∠2=180°,∠1+∠DFE=180
∴∠2=∠DFE
又∵∠3=∠B
∴△BCD∽△EDF,∠EDF=∠BCD
∴DE∥BC,∠AED=∠ACB;
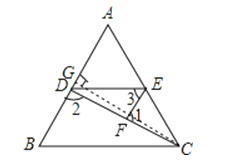
(2)过C作CG⊥AB于G交EF于H
∵EF是△ACD的中位线
∴GH=CH=![]() CG,EF=
CG,EF=![]() AD
AD
又∵四边形ADFE是梯形
∴S四边形ADFE=![]() (AD+EF)×GH=
(AD+EF)×GH=![]() ×
×![]() AD×
AD×![]() CG=
CG=![]() ADCG=4
ADCG=4
∴ADCG=![]()
∴S△ABC=![]() ABCG=
ABCG=![]() ×2ADCG=ADCG
×2ADCG=ADCG
∴S△ABC=![]() .
.
【解析】(1)根据角相等可得出三角相似,进而求出DE∥BC,∠AED=∠ACB;
(2)根据D、E、F分别是AB、AC、CD边上的中点可求出四边形ADFE是梯形,作出三角形的高线即可求出梯形与三角形面积的关系.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①整数和分数统称为有理数;②绝对值是它本身的数只有0;③两数之和一定大于每个加数;④如果两个数积为0,那么至少有一个因数为0;⑤0是最小的有理数,其中正确的个数是( )
A. 2个B. 3个C. 4个D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(p,2)与(﹣3,q)关于原点对称,则p+q=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现定义运算“★”,对于任意实数a、b,都有a★b=a2﹣3a+b,如:3★5=32﹣3×3+5,若x★2=6,则实数x的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( )
A.2.5×10﹣5
B.2.5×105
C.2.5×10﹣6
D.2.5×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】小刚走路时发现自己的影子越走越长,这是因为( )
A.从路灯下走开,离路灯越来越远
B.走到路灯下,离路灯越来越近
C.人与路灯的距离与影子长短无关
D.路灯的灯光越来越亮 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个有理数的奇次幂是正数,那么这个有理数( )
A.一定是正数
B.是正数或负数
C.一定是负数
D.可以是任意有理数
相关试题

