【题目】解方程:3x2+2x+1=0.
参考答案:
【答案】解:∵a=3,b=2,c=1,
∴b2﹣4ac=4﹣4×3×1=﹣8<0.
∴原方程没有实数根.
【解析】根据△>0方程有两个不相等的两个实数根,△=0,方程有两个相等的实数根,△<0,方程没有实数根;△=b2﹣4ac=4﹣4×3×1=﹣8<0,所以原方程没有实数根.
【考点精析】通过灵活运用求根公式,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.

(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标.
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到ADBE,连接AD、DC,∠DCB=30°.求证:DC+BC=AC,即四边形ABCD是勾股四边形.
(4)如图,将△ABC绕顶点B按顺时针方向旋转(0°<a<90°),得到ADBE,连接AD、DC,则∠DCB= °,四边形ABCD是勾股四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,MN∥EF,C为两直线之间一点.
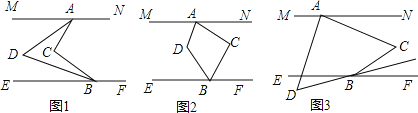
(1)如图1,若∠MAC与∠EBC的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.
(2)如图2,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.
(3)如图3,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请直接写出∠ACB与∠ADB之间的数量关系: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点C在x轴上方,y轴左侧,距离x轴2个单位长度,距离y轴3个单位长度,则点C的坐标为( )
A. (-3,2) B. (-2,-3) C. (-2,3) D. ( 3,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+2)(x﹣1)=x2+mx+n,则m+n= ( )
A. 1 B. ﹣2 C. ﹣1 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数的立方根是-2的数是( )
A. 4 B. -4 C. 8 D. -8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
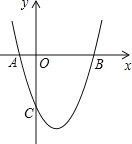
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
相关试题

