【题目】将一次函数y=kx+4(k≠0)的图象称为直线l.
(1)若直线l经过点(2,0),直接写出关于x的不等式kx+4>0的解集;
(2)若直线l经过点(3,﹣2),求这个函数的表达式;
(3)若将直线l向右平移2个单位长度后经过点(5,5),求k的值.
参考答案:
【答案】(1)x<2;(2)y=﹣2x+4;(3)k=![]() .
.
【解析】
(1)根据直线![]() 经过点(2,0)即可得出结论;
经过点(2,0)即可得出结论;
(2)根据题意将(3,﹣2)代入到y=kx+4中,解出k的值即可得出结论;
(3)将点(5,5)向左平移2个单位,得(3,5),将(3,5)代入到y=kx+4中,即可得出结论.
解:(1)不等式kx+4>0的解集为:x<2;
(2)将(3,﹣2)代入到y=kx+4中,
3k+4=﹣2,
解得:k=﹣2.
∴函数表达式为y=﹣2x+4;
(3)将点(5,5)向左平移2个单位,得(3,5),
则y=kx+4的图象经过点(3,5),将(3,5)代入,
解得k=![]() .
.
-
科目: 来源: 题型:
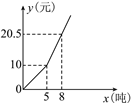
查看答案和解析>>【题目】某市为了节约用水,采用分段收费标准.若某户居民每月应交水费y(元)与用水量x(吨)之间关系的图象如图,根据图象回答:
(1)该市自来水收费时,若使用不足5吨,则每吨收费多少元?超过5吨部分每吨收费多少元?
(2)若某户居民每月用水3.5吨,应交水费多少元?若某月交水费17元,该户居民用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某生物兴趣小组在四天的试验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成如图所示的图象,请根据图象完成下列问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多长时间?
(2)第三天12时这头骆驼的体温是多少?
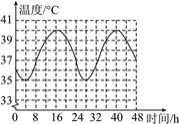
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;(边框线加粗画出,并涂上阴影)

(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请在下列网格图中画出添加小正方体后所得几何体所有可能的左视图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有学生55人,其中男生与女生的人数之比为6:5.
(1)求出该班男生与女生的人数;
(2)学校要从该班选出20人参加学校的合唱团,要求:①男生人数不少于7人;②女生人数超过男生人数2人以上.请问男、女生人数有几种选择方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人先后从公园大门出发,沿绿道向码头步行,乙先到码头并在原地等甲到达.图1是他们行走的路程y(m)与甲出发的时间x(min)之间的函数图象.
(1)求线段AC对应的函数表达式;
(2)写出点B的坐标和它的实际意义;
(3)设d(m)表示甲、乙之间的距离,在图2中画出d与x之间的函数图象(标注必要数据).

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们经常遇到需要分类的问题,画“树形图”可以帮我们不重复、不遗漏地分类.
(例题)在等腰三角形ABC中,若∠A=80°,求∠B的度数.
∠A、∠B都可能是顶角或底角,因此需要分成如图1所示的3类,这样的图就是树形图,据此可求出∠B=
(应用)
(1)已知等腰三角形ABC周长为19,AB=7,仿照例题画出树形图,并直接写出BC的长度;
(2)将一个边长为5、12、13的直角三角形拼上一个三角形后可以拼成一个等腰三角形,图2就是其中的一种拼法,请你画出其他所有可能的情形,并在图上标出所拼成等腰三角形的腰的长度.(选用图3中的备用图画图,每种情形用一个图形单独表示,并用①、②、③…编号,若备用图不够,请自己画图补充)

相关试题

