【题目】实践探究,解决问题
如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ACD . 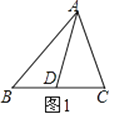
(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,则S阴影=;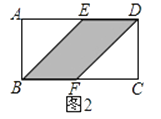
(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴影和S平行四边形ABCD之间满足的关系式为;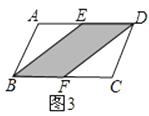
(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴影和S四边形ABCD之间还满足(2)中的关系式吗?若满足,请予以证明,若不满足,说明理由.
解决问题: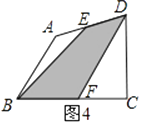
(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和(即S1+S2+S3+S4的值).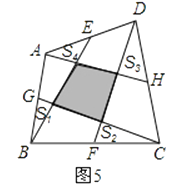
参考答案:
【答案】
(1)16
(2)S阴影= ![]() S平行四边形ABCD
S平行四边形ABCD
(3)
解:满足(2)中的关系式,理由如下:
连接BD,由图1得S△EBD= ![]() S△ABD 同理S△BDF=
S△ABD 同理S△BDF= ![]() S△BDC
S△BDC
∴S四边形EBFD=S△EBD+S△BDF= ![]() S四边形ABCD
S四边形ABCD
(4)
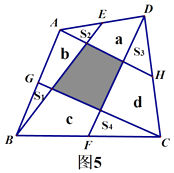
解:设四边形的空白区域分别为a,b,c,d
由上述性质可以得出:
a+S2+S3= ![]() S△ACD①,c+S1+S4=
S△ACD①,c+S1+S4= ![]() S△ACB②,b+S2+S1=
S△ACB②,b+S2+S1= ![]() S△ABD③,d+S4+S3=
S△ABD③,d+S4+S3= ![]() S△ACD④,
S△ACD④,
①+②+③+④得,a+S2+S3+c+S1+S4+b+S2+S1+d+S4+S3=S四边形ABCD⑤
而S四边形ABCD=a+b+c+d+S1+S2+S3+S4+S阴影⑥
所以联立⑤⑥得S1+S2+S3+S4=S阴影=20平方米.
【解析】解:(1)∵E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,
∴S阴影= ![]() ×8×4=16,
×8×4=16,
所以答案是:16;(2)∵E、F分别为平行四边形ABCD的边AD、BC的中点,
∴S阴影= ![]() S平行四边形ABCD;
S平行四边形ABCD;
所以答案是:S阴影= ![]() S平行四边形ABCD;
S平行四边形ABCD;
【考点精析】本题主要考查了矩形的性质的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】京沈高铁赤峰至喀左段于2016年开工建设,天义镇路基桥墩建设初具规模,预计2019年运营,从赤峰出发经宁城至北京500公里,高铁运行速度将是现行普通客车平均速度的5倍,预计开通后,从赤峰出发,某高铁客运专列比普通客车晚3小时开出,但比普通客车早5小时到达北京,求两车的运行速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内一点P(﹣2,3)关于原点对称的点的坐标是( )
A.(3,﹣2)
B.(2,3)
C.(﹣2,﹣3)
D.(2,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】因为(6a3-18a2)÷6a2=________,所以6a3-18a2可因式分解为6a2·________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
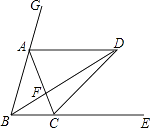
(1)求证:①AB=AD;②CD平分∠ACE.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个完全相同的含30°角的Rt△ABC和Rt△AED叠放在一起,BC交DE于点O,AB交DE于点G,BC交AE于点F,且∠DAB=30°,以下三个结论:①AF⊥BC;②△ADG≌△AFC;③O为BC的中点;④AG=BG.其中正确的个数为( )
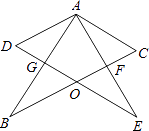
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=
 OB.
OB.(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

相关试题

