【题目】如图所示,两个完全相同的含30°角的Rt△ABC和Rt△AED叠放在一起,BC交DE于点O,AB交DE于点G,BC交AE于点F,且∠DAB=30°,以下三个结论:①AF⊥BC;②△ADG≌△AFC;③O为BC的中点;④AG=BG.其中正确的个数为( ) 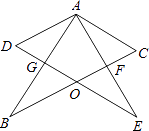
A.1
B.2
C.3
D.4
参考答案:
【答案】D
【解析】解:∵两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°. ∴∠CAF=30°,
∴∠GAF=60°,
∴∠AFB=90°,
∴AF丄BC正确,故①正确,
∵AD=AC,∠DAG=∠CAF,∠D=∠C=60°,
∴△ADG≌△ACF正确,故②正确,
∵△ADG≌△ACF,
∴AG=AF,
∵AO=AO,
∠AGO=∠AFO=90°,
∴△AGO≌△AFO,
∴∠OAF=30°,
∴∠OAC=60°,
∴AO=CO=AC,
∴BO=CO=AO,故③正确,
在Rt△AGE中,∵∠AGE=90°,∠E=30°,
∴AG= ![]() AE,
AE,
∵AB=AE,
∴AG= ![]() AB,
AB,
∴AG=GB,故④正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因为(6a3-18a2)÷6a2=________,所以6a3-18a2可因式分解为6a2·________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实践探究,解决问题
如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ACD .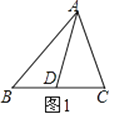
(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,且AB=4,AD=8,则S阴影=;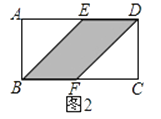
(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴影和S平行四边形ABCD之间满足的关系式为;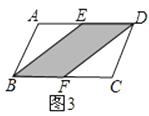
(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴影和S四边形ABCD之间还满足(2)中的关系式吗?若满足,请予以证明,若不满足,说明理由.
解决问题: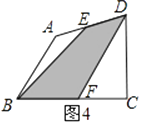
(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和(即S1+S2+S3+S4的值).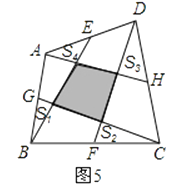
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
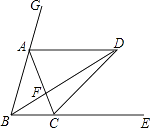
(1)求证:①AB=AD;②CD平分∠ACE.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=
 OB.
OB.(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数据240 000 000用科学记数法表示为( )
A. 24×107B. 0.24×109C. 2.4×108D. 2.48
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在菱形ABCD中,AC=2,BD=2
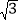 ,AC,BD相交于点O.
,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
相关试题

