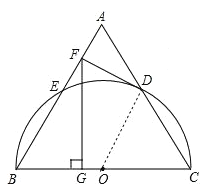
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.
(1)求证:DF⊥AB;
(2)若AF的长为2,求FG的长.

参考答案:
【答案】(1)详见解析;(2)FG=3![]() .
.
【解析】
试题分析:(1)连结OD,根据切线的性质由DF是圆的切线得∠ODF=90°,再根据等边三角形的性质得∠C=∠A=∠B=60°,AB=AC,而OD=OC,所以∠ODC=60°=∠A,于是可判断OD∥AB,根据平行线的性质得DF⊥AB;(2)在Rt△ADF中,由∠A=60°得到∠ADF=30°,根据含30度的直角三角形三边的关系得AD=2AF=4,再证明OD为△ABC的中位线,则AD=CD=4,即AC=8,所以AB=8,BF=AB﹣AF=6,然后在Rt△BFG中,根据正弦的定义计算FG的长.
试题解析:(1)证明:连结OD,如图,
∵DF是圆的切线,
∴OD⊥DF,
∴∠ODF=90°,
∵△ABC为等边三角形,
∴∠C=∠A=∠B=60°,AB=AC,
而OD=OC,
∴∠ODC=60°,
∴∠ODC=∠A,
∴OD∥AB,
∴DF⊥AB;
(2)解:在Rt△ADF中,∠A=60°,
∴∠ADF=30°,
∴AD=2AF=2×2=4,
而OD∥AB,点O为BC的中点,
∴OD为△ABC的中位线,
∴AD=CD=4,即AC=8,
∴AB=8,
∴BF=AB﹣AF=6,
∵FG⊥BC,
∴∠BGF=90°,
在Rt△BFG中,sinB=sin60°=![]() ,
,
∴FG=6×![]() =3
=3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(2a3b-4ab3)·(-0. 5ab)2 .
(2)已知x2+4x-1=0,求代数式(x+2)2-(x+2)(x-2)+x2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:xy3-4xy= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,宏达蔬菜基地内有一块长为216m,宽为108m的长方形土地,三条宽均为xm的田间小路把它分成面积相等的六块,分别种植西红柿、黄瓜、辣椒、芸豆、韭菜、茄子.

(1)求每块种植蔬菜的长方形的面积.(用含x的多项式表示)
(2)当x=1.6m时,求每块种植蔬菜的长方形的面积.(精确到0.01m2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图2,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )

A. ① B. ② C. ①② D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝间距离的最大值为( )

A.5 B.6 C.7 D.10
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了保证安全,某仓库引进A型、B型两台机器人搬运某种有毒货物到仓库存放,这两台机器人充满电后,各能连续工作5h,按照指令,A型机器人于某日零时开始搬运,过了1h,B型机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(kg)与A型机器人搬运时间x(h)之间的关系图象,线段EF表示B种机器人的搬运量yB(kg)与A型机器人的时间x(h)之间的关系图象,根据图象提供的信息解答下列问题:
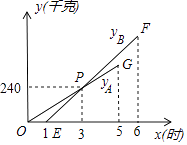
(1)点P表示的意义为:当x=3h时
(2)直接写出线段OG所表示的搬运量与时间x(h)之间的关系式
(3)A型机器人每小时搬运有毒货物kg,B型机器人每小时搬运有毒货物kg.
(4)到工作结束(各5h),A型、B型两台机器人共搬运多少有毒货物?
相关试题

