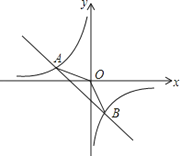
【题目】如图,在平面直角坐标系xOy中,一次函数y![]() =ax+b(a,b为常数,且a≠0)与反比例函数y
=ax+b(a,b为常数,且a≠0)与反比例函数y![]() =
=![]() (m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n).
(m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n).
(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
参考答案:
【答案】(1)反比例函数解析式为y=﹣![]() ;一次函数解析式为y1=﹣x﹣1;(2)
;一次函数解析式为y1=﹣x﹣1;(2)![]() ;(3)x>1.
;(3)x>1.
【解析】试题分析:(1)将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例函数解析式;将B坐标代入反比例解析式中求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出a与b的值,即可确定出一次函数解析式;
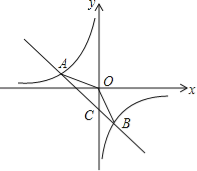
(2)设直线AB与y轴交于点C,求得点C坐标,S△AOB=S△AOC+S△COB,计算即可;
(3)由图象直接可得自变量x的取值范围.
解:(1)∵A(﹣2,1),
∴将A坐标代入反比例函数解析式y2=![]() 中,得m=﹣2,
中,得m=﹣2,
∴反比例函数解析式为y=﹣![]() ;
;
将B坐标代入y=﹣![]() ,得n=﹣2,
,得n=﹣2,
∴B坐标(1,﹣2),
将A与B坐标代入一次函数解析式中,得![]() ,
,
解得a=﹣1,b=﹣1,
∴一次函数解析式为y1=﹣x﹣1;
(2)设直线AB与y轴交于点C,
令x=0,得y=﹣1,
∴点C坐标(0,﹣1),
∴S△AOB=S△AOC+S△COB=![]() ×1×2+
×1×2+![]() ×1×1=
×1×1=![]() ;
;
(3)由图象可得,当y1<y2<0时,自变量x的取值范围x>1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果P(m-1,m)在y轴上,那么点P的坐标是( )
A. (-2,0) B. (0,-2) C. (1,0) D. (0,1)
-
科目: 来源: 题型:
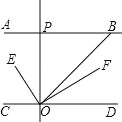
查看答案和解析>>【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
①∠BOE=
 °;
°;②OF平分∠BOD;
③∠POE=∠BOF;
④∠POB=2∠DOF.
其中正确的个数有多少个?( )
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3, 已知A(1,3),A1 (2,3), A2 (4,3), A3 (8,3),B(2,0), B1 (4,0), B2 (8,0), B3 (16,0),观察每次变换前后的三角形有何变化,找出规律,按此变换规律将△OA3B3变换成△OAnBn, ,则An的坐标是_______ ,Bn的坐标是_________ .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将纸片△ABC沿DE折叠使点A落在A′处的位置.
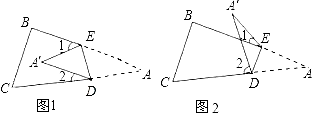
(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是 .
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b为有理数,a>0,b<0,且|a|<|b|,那么a,b,﹣a,﹣b的大小关系是( )
A.b<﹣a<﹣b<a
B.b<﹣b<﹣a<a
C.b<﹣a<a<﹣b
D.﹣a<﹣b<b<a -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
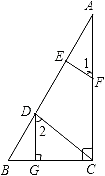
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠ (等量代换)
∴EF∥CD( )
∴∠AEF=∠ ( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
相关试题

