搜索
【题目】若y＝（m+2）x|m|+2x﹣1是二次函数，则m＝_____．
参考答案：
【答案】2．
【解析】
根据形如y=ax2+bx+c(a、b、c是常数，a≠0)的函数，叫做二次函数可得：|m|=2，且m+2≠0，再解即可．
∵y＝（m+2）x|m|+2x﹣1是二次函数，
∴|m|＝2且m+2≠0，
解得：m＝2．
故答案为：2．
-
科目： 来源： 题型：
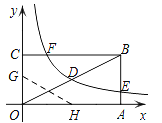
查看答案和解析>>【题目】如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（8，n）在边AB上，反比例函数
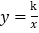（k≠0）在第一象限内的图象经过点D、E，且tan∠BOA=
．（1）求反比例函数的解析式和n的值；
（2）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求G点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】比较大小：﹣（﹣5）〇﹣|﹣5|，“〇”中应该填（ ）
A. ＞B. ＜C. ＝D. 无法比较
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b与反比例函数y=
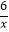（x＞0）的图象交于A（m，6），B（3，n）两点．
（1）求一次函数的解析式；
（2）求△AOB的面积．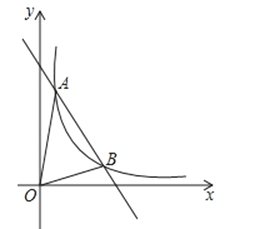
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店需要购进一批电视机和洗衣机，根据市场调查，决定电视机进货量不少于洗衣机进货量的一半．电视机与洗衣机的进价和售价如下表：
类 别
电视机
洗衣机
进价(元/台)
1 800
1 500
售价(元/台)
2 000
1 600
计划购进电视机和洗衣机共 100 台，商店最多可筹集资金161 800 元．
(1)请你帮助商店算一算有多少种进货方案(不考虑除进价之外的其他费用)；
（2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得的利润最多？并求出最大的利润(利润＝售价－进价)．
-
科目： 来源： 题型：
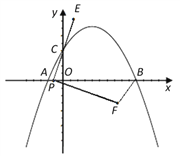
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知点A、B、C的坐标分别为(-1，0)，(5，0)，(0，2)．
（1）求过A、B、C三点的抛物线解析式；
（2）若点P从A点出发，沿x轴正方向以每秒1个单位长度的速度向B点移动，连接PC并延长到点E，使CE=PC，将线段PE绕点P顺时针旋转90°得到线段PF，连接FB．若点P运动的时间为t秒(0≤t≤6)，设△PBF的面积为S；
①求S与t的函数关系式；
②当t是多少时，△PBF的面积最大，最大面积是多少？
（3）点P在移动的过程中，△PBF能否成为直角三角形？若能，直接写出点F的坐标；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知正比例函数y=2x的图象与反比例函数y=
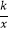（k≠0）在第一象限的图象交于A点，过A点作x轴的垂线，垂足为P点，已知△OAP的面积为1．
（1）求反比例函数的解析式；
（2）如果点B为反比例函数在第一象限图象上的点（点B与点A不重合），且点B的横坐标为2，在x轴上求一点M，使MA+MB最小．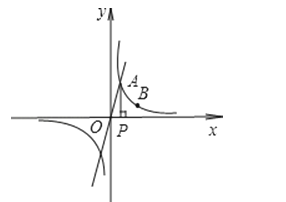
相关试题
