【题目】(1)问题探究
①如图1,在直角△ABC中,∠ABC=90°,AC=5,BC=3,P是AC边上一点,连接BP,则BP的最小值为 .
②如图2,在等腰直角△ABC中,∠ABC=90°,AC=a,求边AB的长度(用含a的代数式表示).
(2)问题解决
如图3,在等腰直角△ABC中,∠ABC=90°,AC=2![]() ,D是边BC的中点,若P是AB边上一点,试求:PD+
,D是边BC的中点,若P是AB边上一点,试求:PD+![]() AP的最小值.
AP的最小值.
参考答案:
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①作BE⊥AC于E,先利用勾股定理求出AB,再利用面积法求出BE,由此得到BP的最小值为BE的长;
②利用AC=a根据勾股定理即可求出AB的长度;
(2)作AH⊥AC,PE⊥AH于E,DF⊥AH于F交AB于T,利用等腰直角三角形的性质得到BT=BD=AT=1,DT=![]() ,再求出TF=
,再求出TF=![]() 得到DP+
得到DP+![]() PA=DP+PE,由此得到DP+PE最小值为DF的长,计算DF即可得到答案.
PA=DP+PE,由此得到DP+PE最小值为DF的长,计算DF即可得到答案.
(1)①如图1中,作BE⊥AC于E.
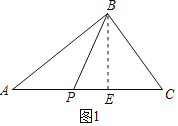
在Rt△ABC中,∵∠ABC=90°,AC=5,BC=3,
∴AB= ![]() ,
,
∵S△ABC=![]() ACBE=
ACBE=![]() ABBC,
ABBC,
∴BE=![]() ,
,
根据垂线段最短可知当BP与BE重合时,PB的值最小,最小值为![]() ,
,
故答案为![]() .
.
②如图2中,
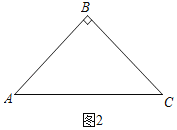
∵∠B=90°,AB=BC,
∴AB2+BC2=AC2,
∴AB2=![]() a2,
a2,
∴AB=![]() 或﹣
或﹣![]() (舍弃),
(舍弃),
∴AB=![]() ;
;
(2)如图3中,作AH⊥AC,PE⊥AH于span>E,DF⊥AH于F交AB于T.
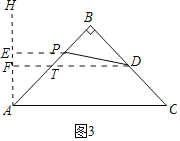
∵△ABC是等腰直角三角形,AC=2![]() ,
,
∴AB=BC=2,∠BAC=∠C=45°,
∵点D是BC的中点,
∴BD=CD=1,
∵DF⊥AH,AC⊥AH,
∴DF∥AC,
∴∠BTD=∠BAC=45°,∠BDT=∠C=45°,
∴∠BTD=∠BDT,
∴BT=BD=AT=1,DT=![]() ,
,
∵AH⊥AC,∠BAC=45°,
∴∠HAC=90°,∠HAT=45°,
∴AF=TF=![]() ,
,
∴PE=![]() PA,
PA,
∴DP+![]() PA=DP+PE,
PA=DP+PE,
根据垂线线段最短可知,当点E与F重合时,PD+![]() PA的值最小,最小值为DF的长=
PA的值最小,最小值为DF的长=![]() +
+![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块形如四边形ABCD的草地中,AB=3m,BC=4m,CD=12m,DA=13m,且∠ABC=90°,要以AC、CD、DA为边制作围栏,问围栏长多少米,草地面积多大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组解应用题:用3辆
 型车和2辆
型车和2辆 型车载满货物一次可运货17吨;用2辆
型车载满货物一次可运货17吨;用2辆 型车和3辆
型车和3辆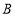 型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用
型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用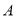 型车
型车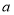 辆,
辆,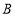 型车
型车 辆,一次运完,且恰好每辆车都载满货物.
辆,一次运完,且恰好每辆车都载满货物.(1)1辆
 型车和1辆
型车和1辆 型车都载满货物一次可分别运货多少吨?
型车都载满货物一次可分别运货多少吨?(2)若
 型车每辆需租金200元/次,
型车每辆需租金200元/次, 型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费.
型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC,D为BC上一点,且DE⊥AB于E,若DE=CD,AB=8cm,则△DEB的周长为( )
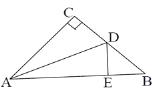
A.4cmB.8cmC.10cmD.14cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某船自西向东航行,在
 处测得某岛
处测得某岛 在北偏东
在北偏东 的方向上,前进
的方向上,前进 海里后到达
海里后到达 ,此时,测得海岛
,此时,测得海岛 在北偏东
在北偏东 的方向上,要使船与海岛
的方向上,要使船与海岛 最近,则船应继续向东前进________海里.
最近,则船应继续向东前进________海里. -
科目: 来源: 题型:
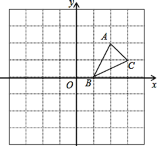
查看答案和解析>>【题目】方格纸中的每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(3,1).
(1)画出△ABC关于y轴对称的△A1B1C1
(2)将△A1B1C1向下平移3个单位后得到△A2B2C2,画出平移后的△A2B2C2,并写出顶点B2的坐标.
相关试题

