【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法——更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也,以等数约之.”意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.例如:求91与56的最大公约数:
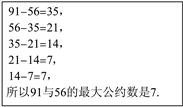
参考答案:
【答案】78,104,143的最大公约数是13.
【解析】
(1)根据题目,首先弄懂题意,然后根据例子写出答案,
(2)可以先求出104与78的最大公约数为26,再利用辗转除法,我们可以求出26与14的最大公约数为13,进而得到答案.
(1)108-45=63,
63-45=18,
45-18=27,
27-18=9,
18-9=9,
所以108与45的最大公约数是9.
(2)先求104与78的最大公约数:
104-78=26,
78-26=52,
52-26=26,
所以104与78的最大公约数是26,
再求26与143的最大公约数:
143-26=117,
117-26=91,
91-26=65,
65-26=39,
39-26=13,
26-13=13,
所以26与143的最大公约数是13.
所以78,104,143的最大公约数是13.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算正确的是( )
A. 2÷
 ×
× =2÷1=2 B. -24+22÷20=-24+4÷20=-20÷20=-1
=2÷1=2 B. -24+22÷20=-24+4÷20=-20÷20=-1C.
 -2×(
-2×( -
- )=
)= -2×(-
-2×(- )=
)= +
+ =
= D. -12÷(6×3)=-2×3=-6
D. -12÷(6×3)=-2×3=-6 -
科目: 来源: 题型:
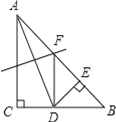
查看答案和解析>>【题目】如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点E,则△DEF的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示.设点A,B,C所对应数的和是p.

(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,外角∠EAB,∠ABF的平分线AD、BD相交于点D,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=
 ,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)= .
.(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1.
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某巡警骑摩托车在一条南北大道上来回巡逻,一天早晨,他从岗亭出发,中午停留在
 处,规定向北方向为正,当天上午连续行驶情况记录如下(单位:千米):+5,﹣4,+3,﹣7,+4,﹣8,+2,﹣1.
处,规定向北方向为正,当天上午连续行驶情况记录如下(单位:千米):+5,﹣4,+3,﹣7,+4,﹣8,+2,﹣1.(1)
 处在岗亭何方?距离岗亭多远?
处在岗亭何方?距离岗亭多远?(2)若摩托车每行驶1千米耗油
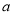 升,这一天上午共耗油多少升?
升,这一天上午共耗油多少升?
相关试题

