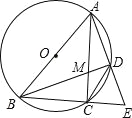
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,点D是劣弧AC上的一点,连结AD并延长与BC的延长线交于点E,AC、BD相交于点M.
(1)求证:BCCE=ACMC;
(2)若点D是劣弧AC的中点,tan∠ACD=![]() ,MDBD=10,求⊙O的半径.
,MDBD=10,求⊙O的半径.
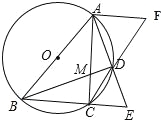
(3)若CD∥AB,过点A作AF∥BC,交CD的延长线于点F,求![]() ﹣
﹣![]() 的值.
的值.
参考答案:
【答案】(1)见试题解析;(2)5;(3)1.
【解析】
试题分析:(1)要证明BCCE=ACMC,即证明![]() =
=![]() ,即证明△CBM∽△CAE;
,即证明△CBM∽△CAE;
(2)因为点D是劣弧![]() 的中点,所以
的中点,所以![]() =
=![]() ,所以∠ABD=∠CAE=∠ACD,进而证明△AMD∽△BAD,可得AD2=MDBD=10,再由tan∠ACD=tan∠ABD=
,所以∠ABD=∠CAE=∠ACD,进而证明△AMD∽△BAD,可得AD2=MDBD=10,再由tan∠ACD=tan∠ABD=![]() ,求出BD的长度,利用勾股定理求出直径AB的长度后,即可求出半径的长度;
,求出BD的长度,利用勾股定理求出直径AB的长度后,即可求出半径的长度;
(3)因为CD∥AB,AF∥BC,所以△CDE∽△BAE,△ADF∽△DEC,利用对边的比相等可得![]() =
=![]() ,所以
,所以![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() .
.
试题解析:(1)∵![]() =
=![]() ,∴∠MBC=∠CAE,∵AB是⊙O的直径,∴∠BCM=∠ACE=90°,∴△CBM∽△CAE,∴
,∴∠MBC=∠CAE,∵AB是⊙O的直径,∴∠BCM=∠ACE=90°,∴△CBM∽△CAE,∴![]() =
=![]() ,∴BCCE=ACMC;
,∴BCCE=ACMC;
(2)∵点D是劣弧![]() 的中点,∴
的中点,∴![]() =
=![]() ;∴∠ABD=∠MBC,∠ACD=∠CAE,∵∠MBC=∠CAE,
;∴∠ABD=∠MBC,∠ACD=∠CAE,∵∠MBC=∠CAE,
∴∠ABD=∠CAE=∠ACD,∵AB是⊙O的直径,∴∠ADB=90°,∴△AMD∽△BAD,
∴![]() =
=![]() ,∴AD2=MDBD=10,∴AD=
,∴AD2=MDBD=10,∴AD=![]() ,∵tan∠ACD=tan∠ABD=
,∵tan∠ACD=tan∠ABD=![]() ,∴
,∴![]() ,
,
∴BD=3![]() ,∵AB2=AD2+BD2,∴AB=
,∵AB2=AD2+BD2,∴AB=![]() =10,∴⊙O的半径为:
=10,∴⊙O的半径为:![]() AB=5;
AB=5;
(3)∵CD∥AB,∴△CDE∽△BAE,∴![]() =
=![]() ,∵AF∥CE,∴△ADF∽△DEC,
,∵AF∥CE,∴△ADF∽△DEC,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游景点的门票售价:成人票每张200元,儿童票每张80元.某日该景点售出门票800张,共得136 000元,求售出成人票多少张?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,位于第二象限的点( )
A.横坐标小于纵坐标B.横坐标大于纵坐标
C.横坐标与纵坐标的和小于0D.横坐标与纵坐标的积大于0
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的底边长为10,则腰长可以是( )
A.1B.3C.5D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=x+b与双曲线y=
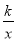 交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.
交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.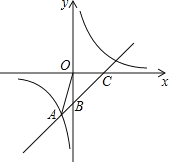
(1)直接写出b= ,m= ;
(2)根据图象直接写出不等式x+b<
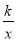 的解集为 ;
的解集为 ;(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在,请求出D的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的长是5cm , 宽是2b cm , 周长为a cm . 列出符合题意的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设P1(x1,y1),P2(x2,y2)是一次函数y=-2x+b图像上的两点,则( )
A.y1>y2B.y1<y2C.当x1<x2时,y1>y2D.当x1<x2时,y1<y2
相关试题

