【题目】如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B;直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q.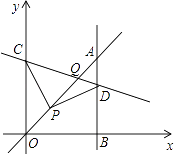
(1)求证:OB=OC;
(2)当点C坐标为(0,3)时,求点Q的坐标;
(3)当△OPC≌△ADP时,直接写出C点的坐标.
参考答案:
【答案】
(1)
证明:过P作GH⊥OC,垂足为G,交AB于H,
过P作PE⊥x轴,垂足为E,
∵AB⊥OB,
∴GH⊥AB,
∵∠CPD=90°,
∴∠GPC+∠DPH=90°,
∠GCP+∠GPC=90°,
∴∠GCP=∠DPH,
又∵∠CGP=∠PHD=90°,PC=PD,
∴△CGP≌△PHD,
∴CG=PH,
∵∠PEB=∠EBH=∠BHP=90°,
∴四边形PEBH为矩形,
∴PH=EB,
∴CG=EB,
∵GH∥OB,OG∥PE,∠GOE=90°,
∴四边形GOEP为矩形,
∵直线OA:y=x,
∴∠GOP=∠POE=45°,
∵∠GPO=∠POE=45°,
∴∠GOP=∠GPO,
∴GO=GP,
∴矩形GOEP为正方形,
∴OG=OE,
∴OG+GC=OE+EB,
即OC=OB
(2)
证明:∵P(1,1),
∴OG=BH=PG=DH=1,
∵C(0,3),
∴OB=OC=3,
∴D(3,2),
设直线CD的解析式为:y=kx+b,
把D(3,2)、C(0,3)代入得: ![]() ,
,
解得 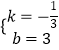 ,
,
∴直线CD的解析式为:y=﹣ ![]() x+3,
x+3,
则 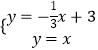 解得
解得 ![]() ,
,
∴Q( ![]() ,
, ![]() )
)
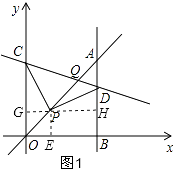
(3)
证明:如图2,过P作GH⊥OC,垂足为G,交AB于H,
设CG=x,则PH=x,OC=x+1,
∵△OPC≌△ADP,
∴AP=OC=x+1,AD=OP= ![]() ,
,
∴AH= ![]() +1,
+1,
在Rt△APH中,由勾股定理得:(x+1)2=x2+( ![]() +1)2,
+1)2,
x= ![]() +1,
+1,
∴C(0,2+ ![]() ).
).
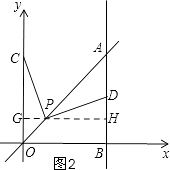
【解析】(1)作辅助线,构建全等三角形,证明CG=EB,证明四边形OGPE为正方形得OG=OE,所以OC=OB;(2)先求点D的坐标,再利用待定系数法求直线CD的解析式,与直线OA的解析式列方程组求出点Q的坐标;(3)设CG=x,根据△OPC≌△ADP表示出直角三角形APH各边的长,利用勾股定理列方程求出x的值,写出点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一节”期间,小明一家自驾游去了离家240千米的某地,如图是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
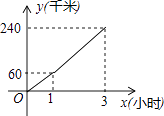
(1)求出y(千米)与x(小时)之间的函数表达式;
(2)他们出发2小时时,离目的地还有多少千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和1个B品牌的计算器共需122元;购买1个A品牌和2个B品牌的计算器共需124元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店举行促销活动,具体办法如下:购买A品牌计算器按原价的九折销售,购买B品牌计算器超出10个以上超出的部分按原价的八折销售,设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过10个,问购买哪种品牌的计算器更合算?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:四边形ABCD是正方形,E是AB边上一点,F是BC延长线上一点,且DE=DF.
(1)如图1,求证:DF⊥DE;
(2)如图2,连接AC,EF交于点M,求证:M是EF的中点.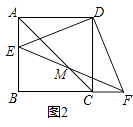
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )

A.48
B.60
C.76
D.80 -
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔首次赛跑“之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米
②兔子和乌龟同时从起点出发
③乌龟在途中休息了10分钟
④兔子在途中750米处追上乌龟
其中说法正确的是( )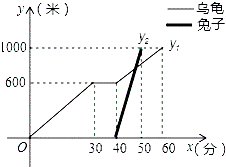
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR,②QP∥AR,③△BPR≌△QPS中一定正确的是( )
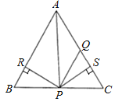
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
相关试题

