【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题: 
(1)本次调查的学生共有人,在扇形统计图中,m的值是;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
参考答案:
【答案】
(1)50;30%
(2)50×20%=10(人),50×10%=5(人),如图所示:

(3)∵5﹣2=3(名),
∴选修书法的5名同学中,有3名男同学,2名女同学,
男1 | 男2 | 男3 | 女1 | 女2 | |
男1 | ﹣﹣﹣ | 男2男1 | 男3男1 | 女1男1 | 女2男1 |
男2 | (男1男2) | ﹣﹣﹣ | 男3男2 | 女1男2 | 女2男2 |
男3 | (男1男3) | 男2男3 | ﹣﹣﹣ | 女1男3 | 女2男3 |
女1 | (男1,女1) | 男2女1 | 男3女1 | ﹣﹣﹣ | 女2女1 |
女2 | (男1女2) | 男2女2 | 男3女2 | 女1女2 | ﹣﹣﹣ |
所有等可能的情况有20种,其中抽取的2名同学恰好是1名男同学和1名女同学的情况有12种,
则P(一男一女)= ![]() =
= ![]() .
.
【解析】解:(1)20÷40%=50(人),15÷50=30%; 所以答案是:50;30%;
【考点精析】掌握扇形统计图和条形统计图是解答本题的根本,需要知道能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则
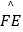 的长为 .
的长为 . 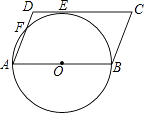
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个关于x的一元二次方程:M:
 N:
N: ,其中
,其中 ,以下列四个结论中,错误的是( )
,以下列四个结论中,错误的是( )A. 如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
B. 如果方程M有两根符号异号,那么方程N的两根符号也异号;
C. 如果5是方程M的一个根,那么
 是方程N的一个根;
是方程N的一个根;D. 如果方程M和方程N有一个相同的根,那么这个根必定是

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4). (Ⅰ)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(Ⅱ)以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.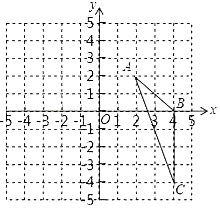
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
(1)某文艺团体组织了一场义演为“希望工程”募捐,共售出1000张门票,已知成人票每张8元,学生票每张5元,共得票款6950元,成人票和学生票各几张
(2)某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润可达4500元;经精加工后销售,每吨利润涨至7500元.当地一家农工商公司收获这种蔬菜140吨,该公司加工的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行.受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司研制了三种可行方案.
方案一:将蔬菜全部进行精加工.没来得及进行精加工的直接出售
方案二:尽可能多地对蔬菜进行粗加工,没有来得及进行加工的蔬菜,在市场上直接销售.
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
相关试题

