【题目】有两个关于x的一元二次方程:M:![]() N:
N:![]() ,其中
,其中![]() ,以下列四个结论中,错误的是( )
,以下列四个结论中,错误的是( )
A. 如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
B. 如果方程M有两根符号异号,那么方程N的两根符号也异号;
C. 如果5是方程M的一个根,那么![]() 是方程N的一个根;
是方程N的一个根;
D. 如果方程M和方程N有一个相同的根,那么这个根必定是![]()
参考答案:
【答案】D
【解析】利用根的判别式判断A;利用根与系数的关系判断B;利用一元二次方程的解的定义判断C与D.
A、如果方程M有两个相等的实数根,那么△=b-4ac=0,所以方程N也有两个相等的实数根,结论正确,不符合题意;
B、如果方程M的两根符号相同,那么方程N的两根符号也相同,那么△=b-4ac ≥0.![]() ,所以a与c符号相同,
,所以a与c符号相同, ![]() ,所以方程N的两根符号也相同,结论正确,不符合题意;
,所以方程N的两根符号也相同,结论正确,不符合题意;
C、如果5是方程M的一个根,那么25a+5b+c=0,两边同时除以25,得![]() ,所以
,所以![]() 是方程N的一个根,结论正确,不符合题意;
是方程N的一个根,结论正确,不符合题意;
D、如果方程M和方程N有一个相同的根,那么![]() ,
,![]() ,由a≠c,得x=1,x=±1,结论错误,符合题意;故选D.
,由a≠c,得x=1,x=±1,结论错误,符合题意;故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有人,在扇形统计图中,m的值是;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4). (Ⅰ)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(Ⅱ)以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.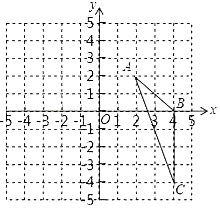
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
(1)某文艺团体组织了一场义演为“希望工程”募捐,共售出1000张门票,已知成人票每张8元,学生票每张5元,共得票款6950元,成人票和学生票各几张
(2)某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润可达4500元;经精加工后销售,每吨利润涨至7500元.当地一家农工商公司收获这种蔬菜140吨,该公司加工的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行.受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司研制了三种可行方案.
方案一:将蔬菜全部进行精加工.没来得及进行精加工的直接出售
方案二:尽可能多地对蔬菜进行粗加工,没有来得及进行加工的蔬菜,在市场上直接销售.
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F. (Ⅰ)试判断直线BC与⊙O的位置关系,并说明理由;
(Ⅱ)若BD=2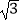 ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).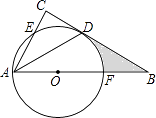
相关试题

