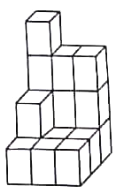
【题目】如图,在一次数学活动课上,张明用17个底面为正方形,且底面边长为![]() ,高为
,高为![]() 的小长方体达成了一个几何体,然后他请王亮用尽可能少的同样的长方体在旁边再搭一个几何体,使王亮所搭的几何体恰好可以和张明所搭的几何体拼成一个大长方体(即拼大长方体时将其中一个几何体翻转,且假定组成每个几何体的小长方体粘合在一起).
的小长方体达成了一个几何体,然后他请王亮用尽可能少的同样的长方体在旁边再搭一个几何体,使王亮所搭的几何体恰好可以和张明所搭的几何体拼成一个大长方体(即拼大长方体时将其中一个几何体翻转,且假定组成每个几何体的小长方体粘合在一起).
(1)王亮至少还需要 个小长方体;
(2)请画出张明所搭几何体的左视图,并计算它的表面积(用含![]() 的代数式表示);
的代数式表示);
(3)请计算(1)条件下王亮所搭几何体的表面积(用含![]() 的代数式表示).
的代数式表示).
参考答案:
【答案】(1)19
(2)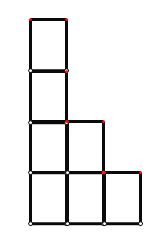 ,
,![]()
(3)![]()
【解析】
(1)确定张明所搭几何体所需的正方体的个数,然后确定两人共搭建几何体所需小立方体的数量,求差即可.
(2)根据图形,画出左视图,计算表面积即可.
(3)画出王亮所搭几何体的俯视图,即可求出表面积.
(1)∵王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体,
∴该长方体需要小立方体![]() 个,
个,
∵张明用17个边长为1的小正方体搭成了一个几何体,
∴王亮至少还需3617=19个小立方体.
(2)张明所搭几何体的左视图有三列,第一列有4个长方形,第二列有2个长方形,第三列有1个长方形:

表面积为: ![]()
(3)王亮所搭几何体的俯视图如图所示,图中数字代表该列小正方体的个数.

故王亮所搭几何体的表面积为:![]()
-
科目: 来源: 题型:
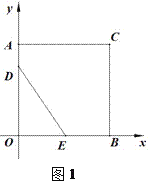
查看答案和解析>>【题目】已知,如图:在直角坐标系中,正方形AOBC的边长为4,点D、E分别是线段AO,OC上的动点,D点由A点向O点运动,速度为每秒1个单位,E点由B点向O点运动,速度为每秒2个单位,当一个点停止运动时,另一个点也随之停止.设运动时间为t(秒)
(1)如图1,当t为何值时,△DOE的面积为6;
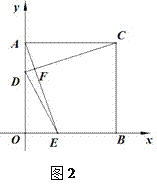
(2)如图2,连结CD,AE交于点F,当t为何值时,CD⊥AE;
(3)如图3,过点D作DG//OB,交BC于点G,连结EG,当D,E在运动过程中,直角坐标系中是否存在点H,使得点D,E,H,G四点构成的四边形为菱形?若存在,求出t的值,并直接写出点G的坐标,若不存在,请说明理由.
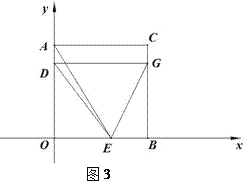
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了数轴后,小亮决定对数轴进行变化应用:
(1)应用一:已知点A在数轴上表示为
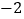 ,数轴上任意一点B表示的数为
,数轴上任意一点B表示的数为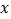 ,则AB两点的距离可以表示为 ;应用这个知识,请写出当
,则AB两点的距离可以表示为 ;应用这个知识,请写出当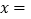 时,
时,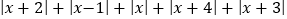 有最小值为 .
有最小值为 .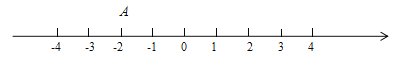
(2)应用二:从数轴上取下一个单位长度的线段,第一次剪掉原长的
 ,第二次剪掉剩下的
,第二次剪掉剩下的 ,依次类推,每次都剪掉剩下的
,依次类推,每次都剪掉剩下的 ,则剪掉5次后剩下线段长度为 ;应用这个原理,请计算:
,则剪掉5次后剩下线段长度为 ;应用这个原理,请计算: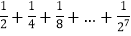 .
.(3)应用三:如图,将一根拉直的细线看作数轴,一个三边长分别为
 的三角形
的三角形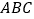 的顶点
的顶点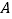 与原点重合,
与原点重合,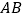 边在数轴正半轴上,将数轴正半轴的线沿
边在数轴正半轴上,将数轴正半轴的线沿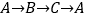 的顺序依次缠绕在三角形
的顺序依次缠绕在三角形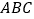 的边上,负半轴的线沿
的边上,负半轴的线沿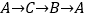 的顺序依次缠绕在三角形
的顺序依次缠绕在三角形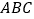 的边上.
的边上.①如果正半轴的线缠绕了5圈,负半轴的线缠绕了3圈,求绕在点
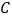 上的所有数之和;
上的所有数之和;②如果正半轴的线不变,将负半轴的线拉长一倍,即原线上的点
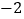 的位置对应着拉长后的数
的位置对应着拉长后的数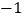 ,并将三角形
,并将三角形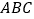 向正半轴平移一个单位后再开始绕,求绕在点
向正半轴平移一个单位后再开始绕,求绕在点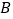 且绝对值不超过100的所有数之和.
且绝对值不超过100的所有数之和.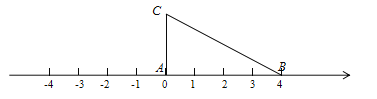
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形OABC在平面直角坐标系中的位置如图所示顶点A(5,0),OB=
 ,P是对角线OB上的一个动点,D(0,1),当CP+DP的值最小时,点P的坐标为( )
,P是对角线OB上的一个动点,D(0,1),当CP+DP的值最小时,点P的坐标为( )
A. (
 ,3
,3 ) B. (
) B. ( ,
, ) C. (1,
) C. (1, ) D. (
) D. ( ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为缓解城市交通压力,决定修建人行天桥,原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°(如图所示).
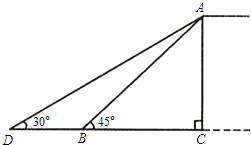
(结果保留根号)
(1)求调整后楼梯AD的长;
(2)求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
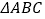 中,
中,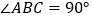 ,BD为AC的中线,过点C作
,BD为AC的中线,过点C作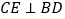 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数
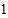 、
、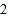 、
、 、
、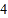 、…、
、…、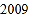 、
、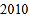 的每个数字前添上“+”或“-”,使得算出的结果是一个最小的非负数,请写出符合条件的式子:________.
的每个数字前添上“+”或“-”,使得算出的结果是一个最小的非负数,请写出符合条件的式子:________.
相关试题

