【题目】为切实减轻中小学生课业负担、全面实施素质教育,某中学对本校学生课业负担情况进行调查. 在本校随机抽取若干名学生进行问卷调查,发现被抽查的学生中,每天完成课外作业时间,最长不足120分钟,没有低于40分钟的,且完成课外作业时间低于60分钟的学生数占被调查人数的10%.现将抽查结果绘制成了一个不完整的频数分布直方图,如图所示.
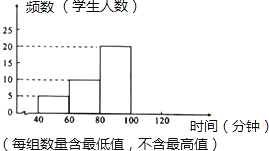
⑴这次被抽查的学生有 人;
⑵请补全频数分布直方图;
⑶被调查这些学生每天完成课外作业时间的中位数在 组(填时间范围);
⑷若该校共有3600名学生,请估计该校大约有多少名学生每天完成课外作业时间在80分钟以上(包括80分钟)
参考答案:
【答案】(1)50 ;(2)第四小组15 ,补全图见解析 ; (3)80-100 ;(4)2520
【解析】试题分析 :(1)根据完成课外作业时间低于60分钟的学生数占被调查人数的10%.可求出抽查的学生人数;
(2)根据总人数,现有人数为补上那15人;
(3)50个数据,第25和26的平均数就是中位数,从表中可看出第25、26人在80-100段里;
(4)先求出50人里学生每天完成课外作业时间在80分钟以上的人的比例,再按比例估算全校的人数.
试题解析:
(1)5÷10%=50
这次被抽查的学生有50人;
(2)如图所示;5035=15
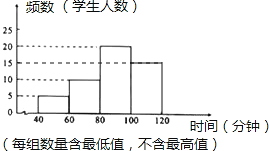
(3)中位数在80至100分钟这一小组内;
(4)由样本知,每天完成课外作业时间在80分钟以上(包括80分钟)的人数有35人,占被调查人数的![]() ,
,
故全校学生中每天完成课外作业时间在80分钟以上(包括80分钟)的人数约有3600×![]() =2520人。
=2520人。
-
科目: 来源: 题型:
查看答案和解析>>【题目】春季已到乍暖还寒,长沙的天气冷热交替,请注意随时增减衣物以防感冒,要反映我市某一周每天的最高气温的变化趋势,根据你所学知识宜采用( )
A.条形统计图B.扇形统计图C.折线统计图D.频数分布统计图
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
【答案】B
【解析】解析:∵2a4+2b4+c4=2a2c2+2b2c2,∴4a4-4a2c2+c4+4b4-4b2c2+c4=0,
∴(2a2-c2)2+(2b2-c2)2=0,∴2a2-c2=0,2b2-c2=0,
∴c=2a,c=2b,
∴a=b,且a2+b2=c2,
∴△ABC为等腰直角三角形.
故选B.
【题型】单选题
【结束】
11【题目】将图1中阴影部分的小长方形变换到图2的位置,你能根据两个图形的面积关系得到的数学公式是_____.

-
科目: 来源: 题型:
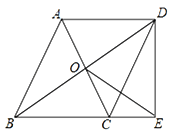
查看答案和解析>>【题目】如图,□ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:△BDE是直角三角形;
(2)如果OE⊥CD,试判断△BDE与△DCE是否相似,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P的坐标为(2+a,3a-6),点P在第四象限且点P到两坐标轴的距离相等,则点P的坐标是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式2a(b+c)-3(b+c)的结果是______.
【答案】(b+c)(2a-3)
【解析】解析:2a(b+c)-3(b+c)=(b+c)(2a-3).
点睛:因式分解的方法:(1)提取公因式法.ma+mb+mc=m(a+b+c).
(2)公式法:完全平方公式,平方差公式.
(3)十字相乘法.
因式分解的时候,要注意整体换元法的灵活应用,训练将一个式子看做一个整体,利用上述方法因式分解的能力.
【题型】填空题
【结束】
17【题目】在我们所学的课本中,多项式与多项式相乘可以用几何图形的面积来表示.例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式:____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在我们所学的课本中,多项式与多项式相乘可以用几何图形的面积来表示.例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式:____________.

【答案】(a+2b)(2a+b)=2a2+5ab+2b2
【解析】试题分析:图②的面积可以用长为a+a+b,宽为b+a+b的长方形面积求出,也可以由四个正方形与5个小长方形的面积之和求出,表示出即可.
解:根据图形列得:(a+2b)(2a+b)=2a2+5ab+2b2.
故答案为:(a+2b)(2a+b)=2a2+5ab+2b2.
考点:多项式乘多项式.
点评:此题考查了多项式乘以多项式法则,熟练掌握法则是解本题的关键.
【题型】填空题
【结束】
18【题目】若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如3=22-12,16=52-32,则3和16是智慧数).已知按从小到大的顺序构成如下数列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,…则第2 013个“智慧数”是______.
相关试题

