【题目】某产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点在原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额-生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?

参考答案:
【答案】(1)![]() ,
, ![]() ;(2)W=
;(2)W=![]() ,年产量为75万件时毛利润最大,最大毛利润为1125万元;(3)1080万元
,年产量为75万件时毛利润最大,最大毛利润为1125万元;(3)1080万元
【解析】(1)先设出函数解析式,再通过待定系数法即可得出函数解析式;(2)根据“毛利润=销售额-生产费用”可求出w与x之间的函数关系式,再通过顶点坐标可得出年产量的值及最大的毛利润;(3)由y=360,得出x的值,再通过关于w的二次函数的增减性即可得出答案.
解:(1)![]() ,
, ![]()
(2)W=![]()
=![]()
=![]()
=![]()
∵![]() <0,
<0,
∴当x=75时,W有最大值1125
∴年产量为75万件时毛利润最大,最大毛利润为1125万元
(3)令y=360,得![]() ,解得x=±60(负值舍去)
,解得x=±60(负值舍去)
由图象可知,当0<y≤360时,0<x≤60
由W=![]() 的性质可知,
的性质可知,
当0<x≤60时,W随x的增大而增大
∴当x=60时,W有最大值1080
∴今年最多可获得毛利润1080万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人同时登西山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:

(1)甲登山的速度是每分钟米,乙在A地提速时距地面的高度b为米.
(2)若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,乙追上了甲此时乙距A地的高度为多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a|=7,|b|=3,且a+b>0,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】代数式3(a+2)用数学语言表示
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
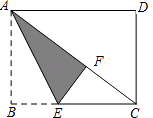
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点O为坐标原点,点P(-2,a), Q(-2,a-5),若△POQ是直角三角形,则点P的坐标不可能为( )
A. (-2,4 )B. (-2, 0)C. (-2, 5)D. (-2,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】说出下列代数式的意义:
(1)a2-b2;
(2)(a-b)2 .
相关试题

