Question

【题目】如图，在矩形纸片ABCD中，已知AD=8，折叠纸片，使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为（ ）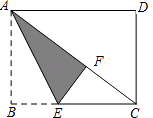

A.3
B.4
C.5
D.6

Answer 1

【答案】D
【解析】解：∵四边形ABCD是矩形，AD=8，
∴BC=8，
∵△AEF是△AEB翻折而成，
∴BE=EF=3，AB=AF，△CEF是直角三角形，
∴CE=8﹣3=5，
在Rt△CEF中，CF= = =4，
设AB=x，
在Rt△ABC中，AC2=AB2+BC2 ， 即（x+4）2=x2+82 ， 解得x=6，
故选：D．
【考点精析】本题主要考查了矩形的性质和翻折变换（折叠问题）的相关知识点，需要掌握矩形的四个角都是直角，矩形的对角线相等；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能正确解答此题．