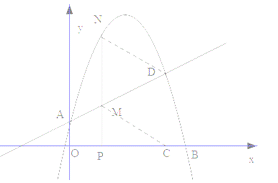
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,与过
,与过![]() 点的直线相交于另一点
点的直线相交于另一点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .
.
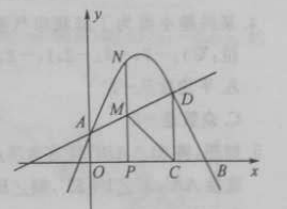
(1)求抛物线的表达式;
(2)点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于
于![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值;
面积的最大值;
(3)若![]() 是
是![]() 轴正半轴上的一动点,设
轴正半轴上的一动点,设![]() 的长为,是否存在,使以点
的长为,是否存在,使以点![]() 为顶点的四边形是平行四边形?若存在,求出的值;若不存在,请说明理由.
为顶点的四边形是平行四边形?若存在,求出的值;若不存在,请说明理由.
参考答案:
【答案】(1) ![]() ;(2)当m=
;(2)当m=![]() 时,
时,![]() ;(3)当
;(3)当![]() 时,以点
时,以点![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
【解析】
试题分析:(1)把点![]() ,
,![]() 代入抛物线
代入抛物线![]() 得方程组,解方程组求得a、b的值,即可求得抛物线的表达式;(2)求的直线AD的表达式,设
得方程组,解方程组求得a、b的值,即可求得抛物线的表达式;(2)求的直线AD的表达式,设![]() (0<m<3),利用m表示出MP和PC的长,再利用三角形的面积公式构建出
(0<m<3),利用m表示出MP和PC的长,再利用三角形的面积公式构建出![]() 面积和m的二次函数模型,利用二次函数的性质即可解决问题;(3)点P在点C的左边和点P在点C的右边两种情况求解.
面积和m的二次函数模型,利用二次函数的性质即可解决问题;(3)点P在点C的左边和点P在点C的右边两种情况求解.
试题解析:
(1)把点![]() ,
,![]() 代入抛物线
代入抛物线![]() 可得,
可得,
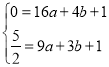
解得,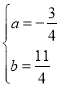
∴![]() ;
;
(2)∵![]() ,
,
∴A(0,1).
设直线AD的表达式为y=kx+b,
把A(0,1),![]() 代入得,
代入得,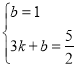 ,
,
解得,![]() ,
,
∴![]()
设![]() (0<m<3),
(0<m<3),
∴MP=![]() ,
,
∵![]() ,
,
∴PC=![]() ,
,
∴![]() ,
,
∴二次函数的顶点坐标为(![]() )
)
即当m=![]() 时,
时,![]() ;
;
(3)存在.
①点P在点C的左边,
∵OP的长为t,设![]() (0<t<3),则
(0<t<3),则![]() ,
,![]() ,
,
∴MN=![]() ,
,
∵MN=CD=![]() ,
,
∴![]() ,
,
∵△=-39,
∴方程无解;
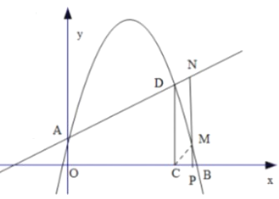
②点P在点C的右边,
OP的长为t,设![]() (t>3),则
(t>3),则![]() ,
,![]() ,
,
∴MN=![]() ,
,
∵MN=CD=![]() ,
,
∴![]() ,
,
解得![]() (舍去),
(舍去),![]() ;
;
综上所述,当![]() 时,以点
时,以点![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生物具有遗传多样性,遗传信息大多储存在DNA分子上.一个DNA分子的直径约为0.0000002cm,这个数量用科学记数法可表示为2×10ncm,则n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4x2﹣8x+4= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x﹣2)(x+3)=x2+mx+n,则mn= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )

A.10
B.12
C.16
D.18 -
科目: 来源: 题型:
查看答案和解析>>【题目】两条平行线间的距离公式 一般地;两条平行线l1:Ax+By+C1=0和l2:Ax+By+C2=0间的距离公式是d=
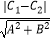 如:求:两条平行线x+3y﹣4=0和2x+6y﹣9=0的距离.
如:求:两条平行线x+3y﹣4=0和2x+6y﹣9=0的距离.
解:将两方程中x,y的系数化成对应相等的形式,得2x+6y﹣8=0和2x+6y﹣9=0,因此,d= 两条平行线l1:3x+4y=10和l2:6x+8y﹣10=0的距离是 .
两条平行线l1:3x+4y=10和l2:6x+8y﹣10=0的距离是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a3a2=a6B. a8÷a2=a4C. (a3)2=a6D. a+2a2=3a2
相关试题

