【题目】如图,一次函数y=kx+b(k<0)与反比例函数y= ![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1) 
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
参考答案:
【答案】
(1)
解:∵点A(4,1)在反比例函数y= ![]() 的图象上,
的图象上,
∴m=4×1=4,
∴反比例函数的解析式为y= ![]() .
.
(2)
解:∵点B在反比例函数y= ![]() 的图象上,
的图象上,
∴设点B的坐标为(n, ![]() ).
).
将y=kx+b代入y= ![]() 中,得:
中,得:
kx+b= ![]() ,整理得:kx2+bx﹣4=0,
,整理得:kx2+bx﹣4=0,
∴4n=﹣ ![]() ,即nk=﹣1①.
,即nk=﹣1①.
令y=kx+b中x=0,则y=b,
即点C的坐标为(0,b),
∴S△BOC= ![]() bn=3,
bn=3,
∴bn=6②.
∵点A(4,1)在一次函数y=kx+b的图象上,
∴1=4k+b③.
联立①②③成方程组,即 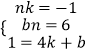 ,
,
解得: 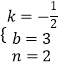 ,
,
∴该一次函数的解析式为y=﹣ ![]() x+3.
x+3.
【解析】(1)由点A的坐标结合反比例函数系数k的几何意义,即可求出m的值;
(2)设点B的坐标为(n, ![]() ),将一次函数解析式代入反比例函数解析式中,利用根与系数的关系可找出n、k的关系,由三角形的面积公式可表示出来b、n的关系,再由点A在一次函数图象上,可找出k、b的关系,联立3个等式为方程组,解方程组即可得出结论.本题考查了反比例函数与一次函数交点的问题、反比例函数系数k的几何意义、三角形的面积公式以及根与系数的关系,解题的关键是:(1)利用反比例函数系数k的几何意义求出m的值;(2)根据各关系量找出关于k、b、n的三元一次方程组.本题属于中档题,难度不大,但考到的知识点较多,解决该题型题目时,综合根与系数的关系、三角形的面积公式以及一次函数上点的坐标特征得出方程组是关键.
),将一次函数解析式代入反比例函数解析式中,利用根与系数的关系可找出n、k的关系,由三角形的面积公式可表示出来b、n的关系,再由点A在一次函数图象上,可找出k、b的关系,联立3个等式为方程组,解方程组即可得出结论.本题考查了反比例函数与一次函数交点的问题、反比例函数系数k的几何意义、三角形的面积公式以及根与系数的关系,解题的关键是:(1)利用反比例函数系数k的几何意义求出m的值;(2)根据各关系量找出关于k、b、n的三元一次方程组.本题属于中档题,难度不大,但考到的知识点较多,解决该题型题目时,综合根与系数的关系、三角形的面积公式以及一次函数上点的坐标特征得出方程组是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣
 x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC
x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC
(1)求△ABC的面积和点C的坐标;
(2)如果在第二象限内有一点P(a,
 ),试用含a的代数式表示四边形ABPO的面积.
),试用含a的代数式表示四边形ABPO的面积. (3)在x轴上是否存在点M,使△MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60
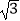 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: 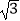 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈  ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).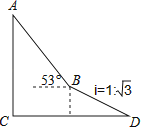
-
科目: 来源: 题型:
查看答案和解析>>【题目】
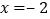 是下列方程中哪一个方程的解( )
是下列方程中哪一个方程的解( )A.
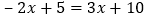 B.
B. 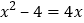 C.
C. 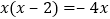 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.

(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG=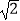 ,DF=2BF,求AH的值.
,DF=2BF,求AH的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在甲处工作的有272人,在乙处工作的有196人,如果要使得乙处工作的人数是甲处工作人数的
 ,应从乙处调多少人到甲处?若设应从乙处调x人到甲处,则下列方程中正确的是( )
,应从乙处调多少人到甲处?若设应从乙处调x人到甲处,则下列方程中正确的是( )A. 272+x=
 (196-x) B.
(196-x) B.  (272-x)=196-x
(272-x)=196-xC.
 (272+x)=196+x D.
(272+x)=196+x D.  (272+x)=196-x
(272+x)=196-x
相关试题

