【题目】在![]() 中,若存在一个内角角度,是另外一个内角角度的
中,若存在一个内角角度,是另外一个内角角度的![]() 倍(
倍(![]() 为大于1的正整数),则称
为大于1的正整数),则称![]() 为
为![]() 倍角三角形.例如,在
倍角三角形.例如,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,可知
,可知![]() ,所以
,所以![]() 为3倍角三角形.
为3倍角三角形.
(1)在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 为________倍角三角形;
为________倍角三角形;
(2)若![]() 是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的
是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的![]() ,求
,求![]() 的最小内角.
的最小内角.
(3)若![]() 是2倍角三角形,且
是2倍角三角形,且![]() ,请直接写出
,请直接写出![]() 的最小内角的取值范围.
的最小内角的取值范围.
参考答案:
【答案】(1)4;(2)![]() 的最小内角为15°或9°或
的最小内角为15°或9°或![]() ;(3)30°<x<45°.
;(3)30°<x<45°.
【解析】
(1)根据三角形内角和定理求出∠C的度数,再根据![]() 倍角三角形的定义判断即可得到答案;
倍角三角形的定义判断即可得到答案;
(2) 根据△DEF是3倍角三角形,必定有一个内角是另一个内角的3倍,然后根据这两个角之间的关系,分情况进行解答即可得到答案;
(3) 可设未知数表示2倍角三角形的各个内角,然后列不等式组确定最小内角的取值范围.
解:(1)∵在![]() 中,
中,![]() ,
,![]() ,
,
∴∠C=180°-55°-25°=100°,
∴∠C=4∠B,
故![]() 为4倍角三角形;
为4倍角三角形;
(2) 设其中一个内角为x°,3倍角为3x°,则另外一个内角为:![]()
①当小的内角的度数是3倍内角的余角的度数的![]() 时,
时,
即:x=![]() (90°-3x),
(90°-3x),
解得:x=15°,
②3倍内角的度数是小内角的余角的度数的![]() 时,
时,
即:3x=![]() (90°-x),解得:x=9°,
(90°-x),解得:x=9°,
③当![]() 时,
时,
解得:![]() ,
,
此时:![]() =
=![]() ,因此为最小内角,
,因此为最小内角,
因此,△DEF的最小内角是9°或15°或![]() .
.
(3) 设最小内角为x,则2倍内角为2x,第三个内角为(180°-3x),由题意得:
2x<90°且180°-3x<90°,
∴30°<x<45°,
答:△MNP的最小内角的取值范围是30°<x<45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.

(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y=
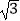 x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为( )
x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为( )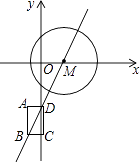
A.(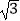 ﹣
﹣  ,﹣
,﹣ 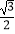 )
)
B.(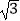 ﹣
﹣  ,﹣
,﹣ 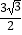 )
)
C.(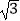 ﹣
﹣  ,﹣
,﹣ 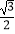 )或(
)或( 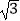 +
+  ,﹣
,﹣ 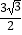 )
)
D.(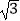 ﹣
﹣  ,﹣
,﹣ 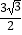 )或(
)或( 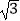 +
+  ,
, 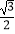 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,点
中,点 为
为 轴上的动点,点
轴上的动点,点 为
为 轴上方的动点,连接
轴上方的动点,连接 ,
, ,
, .
.(1)如图1,当点
 在
在 轴上,且满足
轴上,且满足 的角平分线与
的角平分线与 的角平分线交于点
的角平分线交于点 ,请直接写出
,请直接写出 的度数;
的度数;
(2)如图2,当点
 在
在 轴上,
轴上, 的角平分线与
的角平分线与 的角平分线交于点
的角平分线交于点 ,点
,点 在
在 的延长线上,且满足
的延长线上,且满足 ,求
,求 ;
;
(3)如图3,当点
 在第一象限内,点
在第一象限内,点 是
是 内一点,点
内一点,点 ,
, 分别是线段
分别是线段 ,
, 上一点,满足:
上一点,满足: ,
, ,
, .
.
以下结论:①
 ;②
;② 平分
平分 ;③
;③ 平分
平分 ;④
;④ .
.正确的是:________.(请填写正确结论序号,并选择一个正确的结论证明,简写证明过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,抛物线
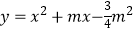 (m>0)与x轴交于A,B两点.若A,B两点到原点的距离分别为OA,OB,且满足
(m>0)与x轴交于A,B两点.若A,B两点到原点的距离分别为OA,OB,且满足 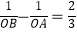 ,则m的值等于 .
,则m的值等于 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是加热食用油的温度变化情况:
时间

0
10
20
30
40
油温
 ℃
℃10
30
50
70
90
王红发现,烧了110
 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )A.没有加热时,油的温度是10℃B.加热50
 ,油的温度是110℃
,油的温度是110℃C.估计这种食用油的沸点温度约是230℃D.每加热10
 ,油的温度升高30℃
,油的温度升高30℃
相关试题

