【题目】在平面直角坐标系![]() 中,点
中,点![]() 为
为![]() 轴上的动点,点
轴上的动点,点![]() 为
为![]() 轴上方的动点,连接
轴上方的动点,连接![]() ,
,![]() ,
,![]() .
.
(1)如图1,当点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() 的角平分线与
的角平分线与![]() 的角平分线交于点
的角平分线交于点![]() ,请直接写出
,请直接写出![]() 的度数;
的度数;

(2)如图2,当点![]() 在
在![]() 轴上,
轴上,![]() 的角平分线与
的角平分线与![]() 的角平分线交于点
的角平分线交于点![]() ,点
,点![]() 在
在![]() 的延长线上,且满足
的延长线上,且满足![]() ,求
,求![]() ;
;

(3)如图3,当点![]() 在第一象限内,点
在第一象限内,点![]() 是
是![]() 内一点,点
内一点,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上一点,满足:
上一点,满足:![]() ,
,![]() ,
,![]() .
.

以下结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() .
.
正确的是:________.(请填写正确结论序号,并选择一个正确的结论证明,简写证明过程).
参考答案:
【答案】(1)135°,(2)2;(3)②③④,理由见详解
【解析】
(1)根据三角形内角和定理(三角形的内角和是180°)和角平分线定理可求∠P的度数,进而得到答案;
(2)根据三角形外角的性质和角平分线定理可求解,进而可以得到答案;
(3)过点P作PF⊥OA于点F,过点P作PE⊥OB于点E,根据全等三角形的性质和角平分线性质,可求解.
解:(1) ∵∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AP平分∠OAB,BP平分∠OBA,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2) ∵BC平分∠ABO,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3) 如图,连接OP,过点P作PF⊥OA于点F,过点P作PE⊥OB于点E,

∵∠ONP+∠OMP=180°,且∠OMP+∠PMF=180°,
∴∠PNO=∠PMF,且PN=PM,∠PEO=∠PFO=90°
∴△PEN≌△PMF(AAS)
∴PE=PF,且PE⊥OB,PF⊥OA
∴OP平分∠AOB,
如上图,作BH平分∠OBA,交OP延长线于点H,连接AH,
∵BH平分∠OBA,OH平分∠BOA,
∴AH平分∠OAB
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点H与点P重合,
∴AP平分∠OAB;BP平分∠OBA,
故②③正确,
∵PE=PF,OP=OP
∴Rt△OPE≌Rt△OPF(HL)
∴OE=OF,且OM<OF=OE<ON
故①错误
如上图,在AB上截取AQ=AM,
∵AM=AQ,∠OAP=∠BAP,AP=AP
∴△MAP≌△QAP(SAS),
∴∠PMA=∠PQA,
∴∠ONP=∠AQP,
∴∠BNP=∠BQP,且BP=BP,∠OBP=∠ABP,
∴△BPN≌△BPQ(AAS),
∴BN=BQ,
∴AB=AQ+BQ=AM+BN,
故④正确
故答案为:②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y=
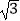 x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为( )
x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为( )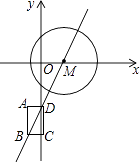
A.(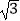 ﹣
﹣  ,﹣
,﹣ 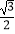 )
)
B.(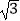 ﹣
﹣  ,﹣
,﹣ 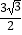 )
)
C.(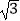 ﹣
﹣  ,﹣
,﹣ 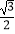 )或(
)或( 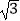 +
+  ,﹣
,﹣ 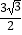 )
)
D.(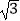 ﹣
﹣  ,﹣
,﹣ 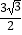 )或(
)或( 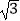 +
+  ,
, 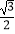 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,若存在一个内角角度,是另外一个内角角度的
中,若存在一个内角角度,是另外一个内角角度的 倍(
倍( 为大于1的正整数),则称
为大于1的正整数),则称 为
为 倍角三角形.例如,在
倍角三角形.例如,在 中,
中, ,
, ,
, ,可知
,可知 ,所以
,所以 为3倍角三角形.
为3倍角三角形.(1)在
 中,
中, ,
, ,则
,则 为________倍角三角形;
为________倍角三角形;(2)若
 是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的
是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的 ,求
,求 的最小内角.
的最小内角.(3)若
 是2倍角三角形,且
是2倍角三角形,且 ,请直接写出
,请直接写出 的最小内角的取值范围.
的最小内角的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,抛物线
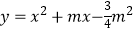 (m>0)与x轴交于A,B两点.若A,B两点到原点的距离分别为OA,OB,且满足
(m>0)与x轴交于A,B两点.若A,B两点到原点的距离分别为OA,OB,且满足 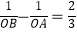 ,则m的值等于 .
,则m的值等于 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是加热食用油的温度变化情况:
时间

0
10
20
30
40
油温
 ℃
℃10
30
50
70
90
王红发现,烧了110
 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )A.没有加热时,油的温度是10℃B.加热50
 ,油的温度是110℃
,油的温度是110℃C.估计这种食用油的沸点温度约是230℃D.每加热10
 ,油的温度升高30℃
,油的温度升高30℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为10厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.设运动时间为t秒.
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,则当t为何值时,能够使△BPE与△CQP全等;此时点Q的运动速度为多少.

相关试题

