【题目】如图,四边形ABCD,AD∥BC,∠B=90°,AD=6,AB=4,BC=9. 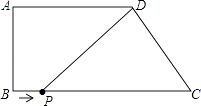
(1)求CD的长为 .
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?
参考答案:
【答案】
(1)5
(2)解:过点D作DE⊥BC,垂足为E,由题意得PC=9﹣t,PE=6﹣t.
当CD=CP时,5=9﹣t,解得t=4;
当CD=PD时,E为PC中点,
∴6﹣t=3,
∴t=3;
当PD=PC时,PD2=PC2,
∴(6﹣t)2+42=(9﹣t)2,
解得t= ![]() .
.
故t的值为t=3或4或 ![]() .
.
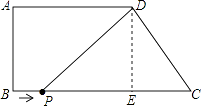
【解析】解:(1)过点D作DE⊥BC,垂足为E,∵AD∥BC,∠B=90°,
∴四边形ABED是矩形,
∴BE=AD=6,DE=AB=4,
∴CE=BC﹣BE=9﹣6=3,
在Rt△DCE中,CD= ![]() =
= ![]() =5.
=5.
所以答案是:5;
【考点精析】利用等腰三角形的判定和勾股定理的概念对题目进行判断即可得到答案,需要熟知如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,牧童在A处放牛,其家在C处,A、C到河岸L的距离分别为AB=2km,CD=4km且,BD=8km.

(1)牧童从A处将牛牵到河边P处饮水后再回到家C,试确定P在何处,所走路程最短?请在图中画出饮水的位置(保留作图痕迹),
不必说明理由.
(2)求出(1)中的最短路程. -
科目: 来源: 题型:
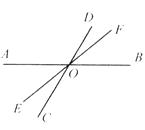
查看答案和解析>>【题目】如图所示,直线AB、CD、EF相交于点O,∠AOE=40°,∠BOC=2∠AOC,求∠DOF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式3a2b﹣a3﹣1+ab2按a的升幂排列是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】生物科技发展公司投资2000万元,研制出一种绿色保健食品.已知该产品的成本为40元/件,试销时,售价不低于成本价,又不高于180元/件.经市场调查知,年销售量y(万件)与销售单价
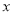 (元/件)的关系满足下表所示的规律.
(元/件)的关系满足下表所示的规律.
(1)y与
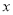 之间的函数关系式是____________,自变量
之间的函数关系式是____________,自变量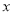 的取值范围为__________;
的取值范围为__________;(2)经测算:年销售量不低于90万件时,每件产品成本降低2元,设销售该产品年获利润为
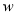 (万元)(
(万元)( 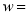 年销售额一成本一投资),求出年销售量低于90万件和不低于90万件时,
年销售额一成本一投资),求出年销售量低于90万件和不低于90万件时, 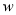 与
与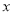 之间的函数关系式;
之间的函数关系式;(3)在(2)的条件下,当销售单价定为多少时,公司销售这种产品年获利润最大?最大利润为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=5,ab=1,则a2+b2的值为( )
A. 6 B. 23 C. 24 D. 27
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小敏将一块三角板中含45°角的顶点放在A上,从AB边开始绕点A逆时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.
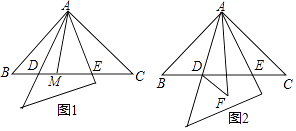
(1)小敏在线段BC上取一点M,连接AM,旋转中发现:若AD平分∠BAM,则AE也平分∠MAC.请你证明小敏发现的结论;
(2)当0°<α≤45°时,小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系:BD2+CE2=DE2 . 同组的小颖和小亮随后想出了相同的方法进行解决:将△ABD沿AD所在的直线对折得到△ADF(如图2);请证明小敏的发现的是正确的.
相关试题

