【题目】如图,△ABC是等边三角形,点D在边AC上(点D不与点A,C重合),点E是射线BC上的一个动点(点E不与点B,C重合),连接DE,以DE为边作等边△DEF,连接CF.
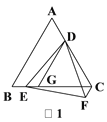
(1)如图1,当DE的延长线与AB的延长线相交,且点C,F在直线DE的同侧时,过点D作DG∥AB,DG交BC于点G,求证:CF=EG;
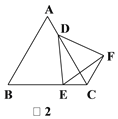
(2)如图2,当DE的反向延长线与AB的反向延长线相交,且点C,F在直线DE的同侧时,求证:CD=CE+CF;
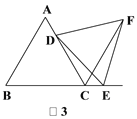
(3)如图3,当DE的反向延长线与线段AB相交,且点C,F在直线DE的异侧时,猜想CD、CE、CF之间的等量关系,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)FC=DC+EC,证明见解析.
【解析】试题分析:(1)根据等边三角形的性质和平行线的性质证出△DCG是等边三角形,得出DC=DG,由△DEF是等边三角形得出DF=DE,然后根据角的关系得出∠EDG=∠FDC,进而得出△EDG≌△FDC,根据全等三角形的性质即可得出结论;
(2)过点D作DG∥AB,DG交BC于点G.同(1)的证明思路可得△EDG≌△FDC.根据全等三角形的对应边相等等量代换即可得出结论;
(3)过点D作DG∥AB,DG交BC于点G.类似于(1)(2)的证明思路可得△EDG≌△FDC.根据全等三角形的对应边相等等量代换即可得出结论.
试题解析:
(1)证明:如图1,∵△ABC是等边三角形,
∴∠B=∠ACB=60°.
∵DG∥AB,
∴∠DGC=∠B.

∴∠DGC=∠DCG=60°.
∴△DGC是等边三角形.
∴DC=DG,∠CDG=60°,
∵△DEF是等边三角形,
∴DE=DF,∠EDF=60°
∴∠EDG=60°-∠GDF,∠FDC=60°-∠GDF,
∴∠EDG=∠FDC,
∴△EDG≌△FDC.
∴FC=EG.
(2)证明:∵△ABC是等边三角形,
∴∠B=∠ACB=60°.
如图2,过点D作DG∥AB,DG交BC于点G.

∴∠DGC=∠B=60°.
∴∠DGC=∠DCG=60°
∴△DGC是等边三角形.
∴CD=DG=CG,∠CDG=60°,
∵△DEF是等边三角形,
∴DE=DF,∠EDF=60°,
∴∠EDG=60°-∠CDE,∠FDC=60°-∠CDE,
∴∠EDG=∠FDC.
∴△EDG≌△FDC.
∴EG=FC.
∵CG=CE+EG,
∴CG=CE+FC.
∴CD=CE+FC.
(3)解:如图3,猜想DC、EC、FC之间的等量关系是FC=DC+EC.
证明如下:
∵△ABC是等边三角形,
∴∠B=∠ACB=60°.
过点D作DG∥AB,DG交BC于点G.

∴∠DGC=∠B.
∴∠DGC=∠DCG=60°
∴△DGC是等边三角形.
∴CD=DG=CG,∠CDG=60°.
∵△DEF是等边三角形,
∴DE=DF,∠EDF=60°,
∴∠EDG=60°+∠CDE,∠FDC=60°+∠CDE,
∴∠EDG=∠FDC.
∴△EDG≌△FDC.
∴EG=FC.
∵EG=EC+CG,
∴FC=EC+DC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:据统计图解答下列问题:

(1)同学们一共调查了多少人?
(2)将条形统计图补充完整.
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传.若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAP+∠APD=180°,∠1=∠2,求证:∠E=∠F.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一楼房AB后有一假山,其坡度为i=1:
 ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)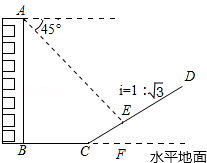
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数
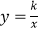 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.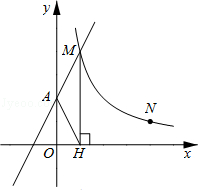
(1)求k的值;
(2)点N(a,1)是反比例函数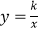 (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K.

(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE= ,AK=2
,AK=2  ,求FG的长.
,求FG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=6,点D为AB边上的一动点(D不与A、B重合),过D作DE∥BC,交AC于点E.把△ADE沿直线DE折叠,点A落在点A′处.连接BA′,设AD=x,△ADE的边DE上的高为y.

(1)求出y与x的函数关系式;
(2)若以点A′、B、D为顶点的三角形与△ABC 相似,求x的值;
(3)当x取何值时,△A′DB是直角三角形.
相关试题

