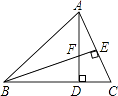
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
参考答案:
【答案】
(1)证明:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∴△ACD∽△BFD.
(2)解:∵tan∠ABD=1,∠ADB=90°
∴ ![]() =1,
=1,
∴AD=BD,
∵△ACD∽△BFD,
∴ ![]() =
= ![]() =1,
=1,
∴BF=AC=3.
【解析】本题考查相似三角形的判定和性质、三角函数等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.(1)由∠C+∠DBF=90°,∠C+∠DAC=90°,推出∠DBF=∠DAC,由此即可证明.(2)先证明AD=BD,由△ACD∽△BFD,得 ![]() =
= ![]() =1,即可解决问题.
=1,即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
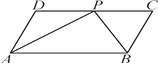
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以直线AB上一点O为端点作射线OC,将一块直角三角板的直角顶点放在O处(注:∠DOE=90°).



(1)如图①,若直角三角板DOE的一边OD放在射线OB上,且∠BOC=60°,求∠COE的度数;
(2)如图②,将三板DOE绕O逆时针转动到某个位置时,若恰好满足5∠COD=∠AOE,且∠BOC=60°,求∠BOD的度数;
(3)如图③,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:

(1)本次调查属于调查,样本容量是;
(2)请补全频数分布直方图中空缺的部分;
(3)求这50名学生每周课外体育活动时间的平均数;
(4)估计全校学生每周课外体育活动时间不少于6小时的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
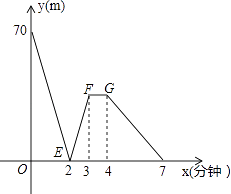
(1)A、B两点之间的距离是米,甲机器人前2分钟的速度为米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段FG∥x轴,则此段时间,甲机器人的速度为米/分;
(4)求A、C两点之间的距离;
(5)直接写出两机器人出发多长时间相距28米.
相关试题

