【题目】如图,在四边形ABCD中,AD∥BC,∠B﹦90°,AB﹦8cm,AD﹦24cm,BC﹦26cm,点p从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t s. 
(1)t为何值时,四边形PQCD为平行四边形?
(2)t为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等)
参考答案:
【答案】
(1)解:运动时间为ts.
AP=t,PD=24﹣t,CQ=3t,
∵经过ts四边形PQCD平行四边形
∴PD=CQ,即24﹣t=3t,解得t=6.
当t=6s时,四边形PQCD是平行四边形
(2)解:如图,过点D作DE⊥BC,则CE=BC﹣AD=2cm
∵当CQ﹣PD=4时,四边形PQCD是等腰梯形.即3t﹣(24﹣t)=4,
∴t=7.
∴经过7s四边形PQCD是等腰梯形.

【解析】(1)根据题意可得PA=t,CQ=3t,则PD=AD﹣PA=24﹣t,当PD=CQ时,四边形PQCD为平行四边形,可得方程24﹣t=3t,解此方程即可求得答案;(2)过点D作DE⊥BC,则CE=BC﹣AD=2cm当CQ﹣PD=4时,四边形PQCD是等腰梯形.即3t﹣(24﹣t)=4,求出t的值即可.
【考点精析】通过灵活运用平行四边形的判定与性质和等腰梯形的性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图正方形ABCD的边长为4,E、F分别为DC、BC中点.

(1)求证:△ADE≌△ABF.
(2)求△AEF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:
(1)求抛物线的解析式.
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.
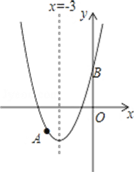
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知A(2,-2),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的点有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的补角是130°,那么这个角的余角的度数是( )
A. 20°B. 40°C. 70°D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A.△AFD≌△DCE
B.AF= ?AD
?AD
C.AB=AF
D.BE=AD﹣DF -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向上平移3个单位后,得到△A1B1C1,请画出△A1B1C1,并直接写出点A1的坐标.
(2)将△ABC绕点O顺时针旋转90°,请画出旋转后的△A2B2C2,并求点B所经过的路径长(结果保留π)

相关试题

