【题目】若α,β是方程x2+2x﹣2020=0的两个实数根,则α2+3α+β的值为______.
参考答案:
【答案】2018
【解析】
先根据一元二次方程的解的定义得到α2+2α-2020=0,则α2+2α=2020,于是α2+3α+β可化为2020+α+β,再利用根与系数的关系得到α+β=-2,然后利用整体代入的方法计算.
∵α是方程x2+2x-2020=0的根,
∴α2+2α-2020=0,
∴α2+2α=2020,
∴α2+3α+β=2020+α+β,
又∵α、β是方程x2+2x-2020=0的两个实数根,
∴α+β=-2,
∴α2+3α+β=2020-2=2018.
故答案为:2018.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,哪些适合抽样调查?哪些适合全面调查?
(1)工厂准备对一批即将出厂的饮料中含有细菌总数的情况进行调查;
(2)小明准备对全班同学所喜爱的球类运动的情况进行调查;
(3)某农田保护区对区内的水稻秧苗的高度进行调查.
-
科目: 来源: 题型:
查看答案和解析>>【题目】假如某市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费. 小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:
(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘坐出租车从汽车站到市政府走了10千米,应付车费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.

第21题图
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a、b被直线c所截,下列说法正确的是( )
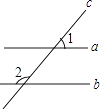
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形纸片ABCD的边长AB=4cm,AD=2cm.同学小明现将该矩形纸片沿EF折痕,使点A与点C重合,折痕后在其一面着色(如图2),观察图形对比前后变化,回答下列问题:
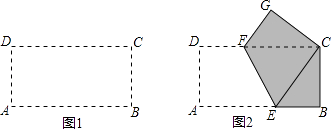
(1)GFFD:(直接填写=、>、<)
(2)判断△CEF的形状,并说明理由;
(3)小明通过此操作有以下两个结论:
①四边形EBCF的面积为4cm2
②整个着色部分的面积为5.5cm2
运用所学知识,请论证小明的结论是否正确. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,E是线段AB上一动点,点F在AD的延长线上运动,且DF=BE.

(1)求证:CE=CF.
(2)当点E在AB上运动时,在AD上取一点G,使∠GCE=45°,试判断BE、EG、GD三条线段的数量关系,并加以证明.
(3)若连接图①中的BD,分别交CE、CG于点M、N,得图②,试根据(2)中的结论说明以线段BM、MN、DN为三边构成的是一个什么形状的三角形?
相关试题

