【题目】如图1，已知抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）、D(2, n)三点．

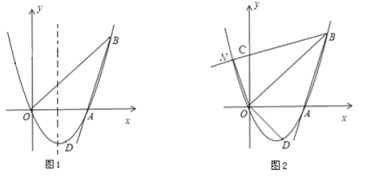
（1）求抛物线的解析式及点D坐标；

（2）点M是抛物线对称轴上一动点，求使BM－AM的值最大时的点M的坐标；

（3）如图2，将射线BA沿BO翻折，交y轴于点C，交抛物线于点N，求点N的坐标；

(4)在（3）的条件下，连结ON,OD，如图2，请求出所有满足△POD∽△NOB的点P坐标（点P、O、D分别与点N、O、B对应）．

参考答案：

【答案】（1）y=x2﹣3x；（2，﹣2）；（2）（，）；（3）（）；（4）（）或（）．

【解析】

试题分析：（1）根据曲线上点的坐标与方程的关系，将（3，0）、B（4，4）代入y=ax2+bx即可求得抛物线的解析式，令x=2，即可求得点D坐标；

（2）抛物线对称轴上使BM－AM的值最大时的点M即直线AB与抛物线对称轴的交点，从而应用待定系数法求出直线AB的解析式，即可求得点M的坐标；

（3）用待定系数法求出直线CB的解析式，由点N在直线CB和抛物线y=x2﹣3x上，即可求出N点的坐标；

（4）应用对称或旋转的性质即可求得点P的坐标.

试题解析：（1）∵抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4），

∴抛物线的解析式是y=x2﹣3x．∴D点的坐标为（2，﹣2）．

（2）设直线AB解析式为：y=kx+m, 将 A（3，0）、B（4，4）代人得

，解得. ∴直线AB解析式为：.

∵抛物线对称轴为，当时， ，

∴当点M（，）时，BM－AM的值最大.

（3）∵直线OB的解析式为y=x，且A（3，0），

根据轴对称性质得出∠CBO=∠ABO，∠COB=∠AOB，OB=OB, ∴△AOB≌△COB.

∴OC=OA. ∴点C（0，3）.

设直线CB的解析式为y=kx+3，过点（4，4），∴直线CB的解析式是.

∵点N在直线CB上，∴设点N（n，）.

又点N在抛物线y=x2﹣3x上，∴，解得：n1=，n2=4（不合题意，舍去）。

∴N点的坐标为（）．

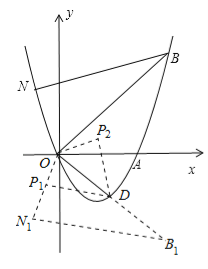
（4）如图，将△NOB沿x轴翻折，得到△N1OB1，则N1（），B1（4，﹣4），

∴O、D、B1都在直线y=﹣x上．

∵△P1OD∽△NOB，△NOB≌△N1OB1，∴△P1OD∽△N1OB1. ∴.

∴点P1的坐标为（）.

将△OP1D沿直线y=﹣x翻折，可得另一个满足条件的点P2（）.

综上所述，点P的坐标是（）或（）．

关闭