【题目】阅读理解:李华是一个勤奋好学的学生,他常常通过书籍、网络等渠道主动学习各种知识.下面是他从网络搜到的两位数乘11的速算法,其口诀是:“头尼一拉,中间相加,满十进一”.例如:①![]() .计算过程:
.计算过程:![]() 两数拉开,中间相加,即
两数拉开,中间相加,即![]() ,最后结果
,最后结果![]() ;②
;②![]() .计算过程:
.计算过程:![]() 两数分开,中间相加,即
两数分开,中间相加,即![]() ,满十进一,最后结果
,满十进一,最后结果![]() .
.
(1)计算:①![]() , ②
, ②![]() _____ ;
_____ ;
(2)若某一个两位数十位数字是![]() ,个位数字是
,个位数字是![]() ,将这个两位数乘
,将这个两位数乘![]() ,得到一个三位数,则根据上述的方法可得,该三位数百位数字是____,十位数字是_____, 个位数字是_____ ; ( 用含
,得到一个三位数,则根据上述的方法可得,该三位数百位数字是____,十位数字是_____, 个位数字是_____ ; ( 用含![]() 的化数式表示)
的化数式表示)
(3)请你结合(2)利用所学的知识解释其中原理.
参考答案:
【答案】(1)①352,②858;(2)![]() ,
,![]() ,
,![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据口诀:“头尼一拉,中间相加,满十进一”,即可求解;(2)由(1)中两位数十位数字是![]() ,个位数字是
,个位数字是![]() ,将这个两位数乘
,将这个两位数乘![]() ,得到一个三位数即可得到结果;(3)结合(2)可得:
,得到一个三位数即可得到结果;(3)结合(2)可得:![]() ,化简得到结论.
,化简得到结论.
解: (1) ![]() .计算过程:
.计算过程:![]() 两数拉开,中间相加,即
两数拉开,中间相加,即![]() ,最后结果
,最后结果![]() ;
;![]() .计算过程:
.计算过程:![]() 两数拉开,中间相加,即
两数拉开,中间相加,即![]() ,满十进一,最后结果
,满十进一,最后结果![]() 故答案为:①
故答案为:①![]() ;②
;②![]() ;
;
(2) 某一个两位数十位数字是![]() ,个位数字是
,个位数字是![]() ,则根据数拉开,中间相加得到:百位数字是:
,则根据数拉开,中间相加得到:百位数字是:![]() ,十位数字是
,十位数字是![]() ,个位数字是:
,个位数字是:![]() ;
;
(3)两位数乘以![]() 可以看成这个两位数乘以
可以看成这个两位数乘以![]() 再加上这个两位数,若两位数的十位数为
再加上这个两位数,若两位数的十位数为![]() ,个位数为
,个位数为![]() ,则
,则![]() 根据上述代数式,不难总结出规律口诀:头尾一拉,中间相加,满十进一.
根据上述代数式,不难总结出规律口诀:头尾一拉,中间相加,满十进一.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.

(1)弦AB=(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数. -
科目: 来源: 题型:
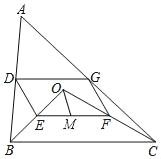
查看答案和解析>>【题目】如图,点O是△ABC内一点,连接OB,OC,并将AB,OB,OC,AC的中点D,E,F,G依次连接得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若OB⊥OC,∠EOM和∠OCB互余,OM=3,求DG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABE中,∠BAE=90°,以AB为直径作⊙O,与BE边相交于点C,过点C作⊙O的切线CD,交AE于点D.

(1)求证:D是AE的中点;
(2)求证:AE2=ECEB. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,OP为一墙面,它与地面OQ垂直,有一根木棒AB如图放置,点C是它的中点,现在将木棒的A点在OP上由A点向下滑动,点B由O点向OQ方向滑动,直到AB横放在地面为止.
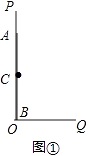
(1)在AB滑动过程中,点C经过的路径可以用下列哪个图象来描述( )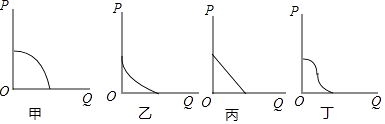
(2)若木棒长度为2m,如图②射线OM与地面夹角∠MOQ=60°,当AB滑动过程中,与OM并于点D,分别求出当AD= 、AD=1、AD=
、AD=1、AD=  时,OD的值.
时,OD的值.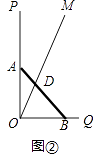
(3)如图③,是一个城市下水道,下水道入口宽40cm,下水道水平段高度为40cm,现在要想把整根木棒AB通入下水道水平段进行工作,那么这根木棒最长可以是(cm)(直接写出结果,结果四舍五入取整数).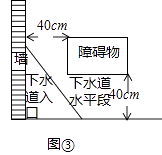
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.以下是甲、乙两同学的作业:
甲:(1)以点C为圆心,AB长为半径画弧;
(2)以点A为圆心,BC长为半径画弧;
(3)两弧在BC上方交于点D,连接AD,CD,四边形ABCD即为所求(如图1)
乙:(1)连接AC,作线段AC的垂直平分线,交AC于点M;
(2)连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD,四边形ABCD即为所求(如图2).
对于两人的作业,下列说法正确的是( )


A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:对于函数y=ax2+bx+c(a≠0),当t1≤x≤t2时,求y的最值时,主要取决于对称轴x=﹣
 是否在t1≤x≤t2的范围和a的正负:①当对称轴x=﹣
是否在t1≤x≤t2的范围和a的正负:①当对称轴x=﹣  在t1≤x≤t2之内且a>0时,则x=﹣
在t1≤x≤t2之内且a>0时,则x=﹣  时y有最小值,x=t1或x=t2时y有最大值;②当对称轴x=﹣
时y有最小值,x=t1或x=t2时y有最大值;②当对称轴x=﹣  在t1≤x≤t2之内且a<0时,则x=﹣
在t1≤x≤t2之内且a<0时,则x=﹣  时y有最大值,x=t1或x=t2时y有最小值;③当对称轴x=﹣
时y有最大值,x=t1或x=t2时y有最小值;③当对称轴x=﹣  不在t1≤x≤t2之内,则函数在x=t1或x=t2时y有最值.
不在t1≤x≤t2之内,则函数在x=t1或x=t2时y有最值.
解决问题:
设二次函数y1=a(x﹣2)2+c(a≠0)的图象与y轴的交点为(0,1),且2a+c=0.
(1)求a、c的值;
(2)当﹣2≤x≤1时,直接写出函数的最大值和最小值;
(3)对于任意实数k,规定:当﹣2≤x≤1时,关于x的函数y2=y1﹣kx的最小值称为k的“特别值”,记作g(k),求g(k)的解析式;
(4)在(3)的条件下,当“特别值”g(k)=1时,求k的值.
相关试题

