【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积![]() =4.
=4.
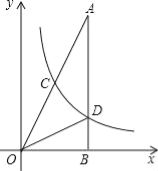
(1)求直线AO的解析式;
(2)求反比例函数解析式;
(3)求点C的坐标.
参考答案:
【答案】(1)y=2x;(2)y=![]() ;(3)(2,4)
;(3)(2,4)
【解析】
试题分析:(1)首先根据题意确定A点坐标,然后设直线AO的解析式为y=kx,再把A点坐标代入可得k的值,进而可得函数解析式;
(2)根据△BOD的面积![]() =4可得D点坐标,再把D点坐标代入y=
=4可得D点坐标,再把D点坐标代入y=![]() 可得k的值,进而可得函数解析式;
可得k的值,进而可得函数解析式;
(3)点C是正比例函数和反比例函数的交点,联立两个函数解析式,然后再解可得C点坐标.
试题解析:(1)∵OB=4,AB=8,∠ABO=90°,
∴A点坐标为(4,8),
设直线AO的解析式为y=kx,
则4k=8,解得k=2,
即直线AO的解析式为y=2x;
(2)∵OB=4,S△BOD=4,∠ABO=90°,
∴D点坐标为(4,2),
点D(4,2)代入y=![]() ,
,
则2=![]() ,解得k=8,
,解得k=8,
∴反比例函数解析式为y=![]() ;
;
(3)直线y=2x与反比例函数y=![]() 构成方程组为
构成方程组为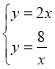 ,
,
解得 ,
,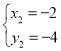 (舍去),
(舍去),
∴C点坐标为(2,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,十位数字与个位数字之和是5,把这个两位数的个位数字与十位数字对调后,所得的新两位数与原来两位数的乘积为736,求原来的两位数.
-
科目: 来源: 题型:
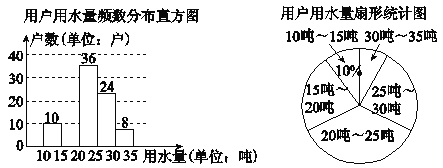
查看答案和解析>>【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是________;
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
-
科目: 来源: 题型:
查看答案和解析>>【题目】课前预习是学习数学的重要环节,为了了解所教班级学生完成数学课前预习的具体情况,王老师对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)王老师一共调查了多少名同学?
(2)C类女生有 名,D类男生有 名,将上面条形统计图补充完整;
(3)为了共同进步,王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列所述图形中,是中心对称图形的是( )
A. 直角三角形 B. 平行四边形 C. 正五边形 D. 正三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
A. (﹣2,﹣1) B. (2,﹣1) C. (﹣2,1) D. (1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地某日最高气温27℃,最低15℃,最高气温比最低气温高( )
A. 22℃ B. 12℃ C. 15℃ D. 14℃
相关试题

