【题目】如图,正方形ABCD的对角线相交于点O,点O是正方形![]() 的一个顶点.如果两个正方形的边长都等于2,那么正方形
的一个顶点.如果两个正方形的边长都等于2,那么正方形![]() 绕O点无论怎样转动,两个正方形重叠的部分的面积是_____________.
绕O点无论怎样转动,两个正方形重叠的部分的面积是_____________.

参考答案:
【答案】1
【解析】如图,连接AC,BD,正方形ABCD的对角线相交于点O,
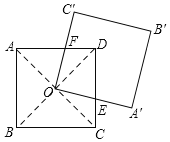
∴∠ODE=∠OAF=45°,OA=OD,∠AOD=90°,
∵∠EOF=∠DOE+∠DOF=90°,∠AOD=∠DOF+∠AOF=90°,
∴∠DOE=∠AOF,
在△DOE和△AOF中,
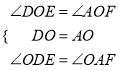 ,
,
∴△DOE≌△AOF(ASA),
∴S△AOF=S△DOE,
∴四边形OEDF的面积=S△DOE+S△DOF=S△AOF+S△DOF=S△AOD,
∵S△AOD=![]() S正方形ABCD=
S正方形ABCD=![]() ×2×2=1,
×2×2=1,
∴四边形OEDF的面积为1,即两个正方形重叠部分的面积为1.
故答案为:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第二象限,P到x轴的距离是2,到y轴的距离是3,P的坐标为___________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有三个球,其中2个红球,1个白球,它们除颜色不同外其余都相同:
(1)摸出一个球记下颜色后放回,并搅匀,再摸出一个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(2)现再将n个白球放入布袋中搅匀后使摸出一个球是白球的概率为
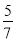 ,求n的值.
,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:

(1)当行使8千米时,收费应为 元;
(2)从图象上你能获得哪些信息?(请写出2条)
① ________
②____________________________
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC交⊙O与点E。
(1)AB与AC的大小有什么关系?为什么?
(2)按角分类, 请你判断△ABC属于哪一类三角形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点(﹣1,﹣5),且与正比例函数y=
 x的图象相交于点(2,a).
x的图象相交于点(2,a).(1)求实数a的值及一次函数的解析式;
(2)求这两个函数图象与x轴所围成的三角形面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P为直线l外一点,A,B,C为直线l上三点,且PA=8cm,PB=7cm,PC=5cm,则点P到直线l的距离为( )
A.5cmB.7cmC.8cmD.不大于5cm
相关试题

