【题目】如图,已知数轴上有![]() 三点,分别表示有理数
三点,分别表示有理数![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度向终点
出发,以每秒1个单位的速度向终点![]() 移动,当点
移动,当点![]() 运动到
运动到![]() 点时,点
点时,点![]() 从
从![]() 点出发,以每秒3个单位的速度向
点出发,以每秒3个单位的速度向![]() 点运动.
点运动.
(1)![]() 点出发3秒后所到的点表示的数为______,此时
点出发3秒后所到的点表示的数为______,此时![]() 两点的距离为_________.
两点的距离为_________.
(2)问当点![]() 从点
从点![]() 点出发几秒钟时,能追上点
点出发几秒钟时,能追上点![]() ?
?
(3)问当点![]() 从点
从点![]() 点出发几秒钟时,点
点出发几秒钟时,点![]() 和点
和点![]() 相距2个单位长度?直接写出此时点
相距2个单位长度?直接写出此时点![]() 在数轴上表示的有理数.
在数轴上表示的有理数.

参考答案:
【答案】(1)-17;10;(2)8(3)当点Q从A点出发7秒和9秒时,点P和点Q相距2个单位长度,此时点Q在数轴上表示的有理数分别为5和1.
【解析】
(1)根据题意得到![]() 点出发3秒后所到的点表示的数与此时P点所表示的数即可求解;
点出发3秒后所到的点表示的数与此时P点所表示的数即可求解;
(2)设x秒可以追上,根据题意列出方程即可求解;
(3)分两种情况:点Q追上点P之前相距2个单位长度.设此时点Q从A点出发t秒钟.根据点P和点Q相距2个单位长度列出方程(16+t)-3t=2;点Q追上点P之后相距2个单位长度.设此时点Q从A点出发m秒钟.根据点P和点Q相距2个单位长度列出方程3m-(16+m)=2,故可求解.
(1)依题意得![]() 点出发3秒后所到的点表示的数为-26+3×3=-17;
点出发3秒后所到的点表示的数为-26+3×3=-17;
此时P点所表示的数为-10+3=-7
![]() 两点的距离为-7-(-17)=10;
两点的距离为-7-(-17)=10;
故答案为:-17;10;
(2)设x秒可以追上,根据题意得3x-x=(-10)-( -26)
解得x=8
故点![]() 从点
从点![]() 点出发8秒钟时,能追上点
点出发8秒钟时,能追上点![]() ;
;
(3)有两种情况:
①点Q追上点P之前相距2个单位长度。设此时点Q从A点出发t秒钟。
依题意,得(16+t)3t=2,
解得,t=7.
此时点Q在数轴上表示的有理数为-26+7×3=5;
②点Q追上点P之后相距2个单位长度。设此时点Q从A点出发m秒钟。
依题意,得3m(16+m)=2,
解得,m=9.
此时点Q在数轴上表示的有理数为-26+9×3=1.
综上所述,当点Q从A点出发7秒和9秒时,点P和点Q相距2个单位长度,此时点Q在数轴上表示的有理数分别为5和1.
-
科目: 来源: 题型:
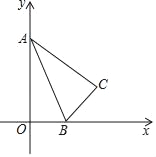
查看答案和解析>>【题目】如图,Rt△ABC中,BC=4,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
(1)AB中点P经过的路径长_____.
(2)点C运动的路径长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点M、N和∠AOB求作一点P,使P到点M、N的距离相等,且到∠AOB的两边的距离相等.(尺规作图,不写做法,保留作图痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是( )

A.1.5B.1.8C.2D.2.5
-
科目: 来源: 题型:
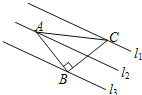
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是_____.
相关试题

