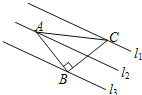
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是_____.
参考答案:
【答案】![]() .
.
【解析】
作辅助线,构建平行线的距离,由已知得:FC=1+2=3,AE=2,根据AAS证明△AEB≌△BFC,得BE=FC=3,先由勾股定理求得AB=![]() ,所以BC=
,所以BC=![]() ,则由勾股定理可以求得AC的长.
,则由勾股定理可以求得AC的长.
解:分别过A、C作l3的垂线AE、CF,垂足分别为E、F,交l2于M,
∵l2∥l3,
∴CF⊥l2,
∴∠CBF+∠BCF=90°,
∵∠ABC=90°,
∴∠CBF+∠ABE=90°,
∴∠BCF=∠ABE,
∵AB=BC,∠AEB=∠BFC=90°,
∴△AEB≌△BFC,
∴BE=FC,
∵l1,l2之间的距离为1,l2,l3之间的距离为2,
∴FC=1+2=3,AE=2,
∴BE=FC=3,
由勾股定理得:AB=![]() =
=![]() =
=![]() ,
,
∴AB=BC=![]() ,
,
∴AC=![]() =
=![]() =
=![]() ,
,
故答案为:![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上有
 三点,分别表示有理数
三点,分别表示有理数 ,动点
,动点 从点
从点 出发,以每秒1个单位的速度向终点
出发,以每秒1个单位的速度向终点 移动,当点
移动,当点 运动到
运动到 点时,点
点时,点 从
从 点出发,以每秒3个单位的速度向
点出发,以每秒3个单位的速度向 点运动.
点运动.(1)
 点出发3秒后所到的点表示的数为______,此时
点出发3秒后所到的点表示的数为______,此时 两点的距离为_________.
两点的距离为_________.(2)问当点
 从点
从点 点出发几秒钟时,能追上点
点出发几秒钟时,能追上点 ?
?(3)问当点
 从点
从点 点出发几秒钟时,点
点出发几秒钟时,点 和点
和点 相距2个单位长度?直接写出此时点
相距2个单位长度?直接写出此时点 在数轴上表示的有理数.
在数轴上表示的有理数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点M、N和∠AOB求作一点P,使P到点M、N的距离相等,且到∠AOB的两边的距离相等.(尺规作图,不写做法,保留作图痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是( )

A.1.5B.1.8C.2D.2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
 ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,过顶点A的直线DE∥BC,∠ABC、∠ACB的平分线分别交DE于点E、D,若AC=3,AB=4,则DE的长为( ).

A. 1B. 3C. 4D. 7
相关试题

