【题目】如图,在边长为4的正方形ABCD中,E是CD的中点,F是BC上的一点,且∠AEF=90°,延长AE交BC的延长线于点G.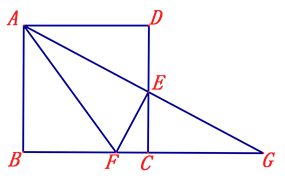
(1)求GE的长;
(2)求证:AE平分∠DAF;
(3)求CF的长.
参考答案:
【答案】
(1)
解:在正方形ABCD中,∠D=90°,AD∥BC
∴∠D=∠DCG=90°,∠DAE=∠G
∵E是CD的中点
∴DE=CE
∴△ADE≌△GCE
∴AD=CG
∵AD=DC=4
∴CG=4,CE=2
在Rt△GCE中,
∴GE= ![]()
(2)
证明:由(1)得:△ADE≌△GCE
∴AE=GE
∵∠AEF=90°
∴EF垂直平分AG
∴AF=GF
∴∠FAE=∠G
∵∠DAE=∠G
∴∠FAE=∠DAE
∴AE平分∠DAF
(3)
解:在正方形ABCD中
∠B=∠BCD=∠D=90°,AB=BC=CD=DA=4
∴DE=CE=2
设CF=x,则BF=4-x
根据勾股定理得:
AF2=AB2+ BF2=42+(4-x)2=32-8x+x2
EF2=CF2+ CE2=x2+22= x2+4
AE2=AD2+ DE2=42+22=20
在Rt△AEF中,AF2= EF2+ AE2
∴32-8x+ x2= x2+4+20
解得:x=1
∴CF=1
【解析】(1)由正方形的性质可以得到△ADE≌△GCE(AAS),根据全等三角形的性质可以得AD=CG;在Rt△GCE中,由勾股定理得到GE长。
(2)由(1)得:△ADE≌△GCE,根据全等三角形的性质可以得AE=GE;再∠AEF=90°,由等腰三角形的性质三线合一可以得到EF垂直平分AG,
AF=GF;再根据等边对等角得∠FAE=∠G,由等量代换可以∠FAE=∠DAE;即AE平分∠DAF。
(3)设CF=x,则BF=4-x,由勾股定理得:AF2=AB2+ BF2=42+(4-x)2=32-8x+x2;EF2=CF2+ CE2=x2+22= x2+4;AE2=AD2+ DE2=42+22=20;
在Rt△AEF中,由AF2= EF2+ AE2解得x=1,即CF=1
【考点精析】根据题目的已知条件,利用角的平分线和等腰三角形的性质的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点.

(1)求证:EN与DM互相平分;
(2)若AB=AC,判断四边形DEMN的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=mx+5的图象经过点A(1,4)、B(n , 2).
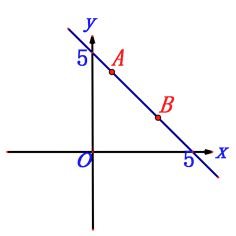
(1)求m、n的值;
(2)当函数图象在第一象限时,自变量x的取值范围是什么?
(3)在x轴上找一点P,使PA+PB最短。求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】a 和5a大小比较是( )
A. a 小于5a
B. a 等于5a
C. a 大于5a
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=-3(x-6)2+9的顶点坐标是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中数据不在分点上,对图中提供的信息作出如下的判断:
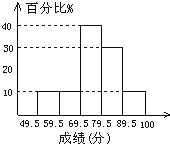
②成绩在79.5~89.5分段的人数占30%;
③成绩在79.5分以上的学生有20人;
④本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】方程2x2+1=3x的二次项系数和一次项系数分别为( )
A.2 和 3B.2 和﹣3C.2 和﹣1D.2 和 1
相关试题

