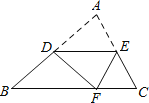
【题目】如图,在△ABC中,∠A=70°∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.
参考答案:
【答案】110°或50°.
【解析】
由内角和定理得出∠C=60°,根据翻折变换的性质知∠DFE=∠A=70°,再分∠EFC=90°和∠FEC=90°两种情况,先求出∠DFC度数,继而由∠BDF=∠DFC﹣∠B可得答案.
∵△ABC中,∠A=70°、∠B=50°,∴∠C=180°﹣∠A﹣∠B=60°,由翻折性质知∠DFE=∠A=70°,分两种情况讨论:
①当∠EFC=90°时,∠DFC=∠DFE+∠EFC=160°,则∠BDF=∠DFC﹣∠B=110°;
②当∠FEC=90°时,∠EFC=180°﹣∠FEC﹣∠C=30°,∴∠DFC=∠DFE+∠EFC=100°,∠BDF=∠DFC﹣∠B=50°;
综上:∠BDF的度数为110°或50°.
故答案为:110°或50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠B=∠C=65°,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )

A.

B.

C.

D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )

A. 1 B.
 C.
C.  D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=6cm , AC=12cm , 动点M从点A出发,以1cm∕秒的速度向点B运动,动点N从点C出发,以2cm∕秒的速度向点A运动,若两点同时运动,是否存在某一时刻t , 使得以点A、M、N为顶点的三角形与△ABC相似,若存在,求出t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次根式
 与
与  能够合并,能否由此确定a=1?若能,请说明理由;不能,请举一个反例说明.
能够合并,能否由此确定a=1?若能,请说明理由;不能,请举一个反例说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD中,AB=1,在BC上取一点E , 沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( ).

A.
B.
C.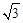
D.2 -
科目: 来源: 题型:
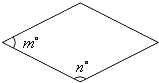
查看答案和解析>>【题目】如图,菱形,矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.设菱形相邻两个内角的度数分别为m和n , 将菱形的“接近度”定义为|m-n|,于是,|m-n|越小,菱形越接近于正方形.若菱形的一个内角为70°,则该菱形的“接近度”等于;当菱形的“接近度”等于时,菱形是正方形.
相关试题

