【题目】如图,⊙O的直径AB=10,C、D是圆上的两点,且![]() .设过点D的切线ED交AC的延长线于点F.连接OC交AD于点G.
.设过点D的切线ED交AC的延长线于点F.连接OC交AD于点G.

(1)求证:DF⊥AF.
(2)求OG的长.
参考答案:
【答案】(1)证明见解析
(2)OG=![]() 。
。
【解析】
试题分析:(1)连接BD,根据![]() ,可得∠CAD=∠DAB=30°,∠ABD=60°,从而可得∠AFD=90°。
,可得∠CAD=∠DAB=30°,∠ABD=60°,从而可得∠AFD=90°。
(2)根据垂径定理可得OG垂直平分AD,继而可判断OG是△ABD的中位线,在Rt△ABD中求出BD,即可得出OG。
解:(1)证明:连接BD,

∵AB是⊙O的直径,![]() ,
,
∴∠CAD=∠DAB=30°,∠ABD=60°。
∵ED是⊙O的切线,∴∠ADF=∠ABD=60°。
∴∠CAD+∠ADF=90°。∴∠AFD=90°。
∴DF⊥AF。
(2)在Rt△ABD中,∠BAD=30°,AB=10,∴BD=5。
∵![]() ,∴OG垂直平分AD。
,∴OG垂直平分AD。
∴OG是△ABD的中位线,∴OG=![]() BD=
BD=![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,已知AB是⊙O直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C作⊙O的切线与ED的延长线交于点P.

(1)求证:PC=PG;
(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG、BF、BO三者之间的数量关系,并写出证明过程;
(3)在满足(2)的条件下,已知⊙O的半径为5,若点O到BC的距离为
 时,求弦ED的长.
时,求弦ED的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形的三个顶点距离相等的点是( )
A. 三条角平分线的交点
B. 三条边的垂直平分线的交点
C. 三条高的交点
D. 三条中线的交点
-
科目: 来源: 题型:
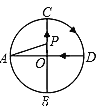
查看答案和解析>>【题目】如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是 ( )
A.
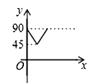 B.
B. 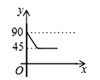 C.
C. 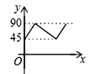 D.
D. 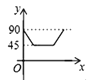
-
科目: 来源: 题型:
查看答案和解析>>【题目】校园里栽下一棵小树高1.8 米,以后每年长0.3米,则n年后的树高L米与年数n年之间的关系式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】七边形剪去一角后所形成的多边形的外角和是_______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】实践:如图△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)作∠BAC的平分线,交BC于点O.
(2)以O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)AB与⊙O的位置关系是_____ .(直接写出答案)
(2)若AC=5,BC=12,求⊙O 的半径.

相关试题

