Question

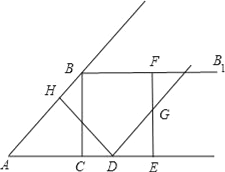
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB1∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t秒．

（1）当t为何值时，AD=AB，并求出此时DE的长度；

（2）当△DEG与△ACB相似时，求t的值．

Answer 1

【答案】（1）当t=1时，AD=AB，AE=1；

（2）当t=或 或 或 时，△DEG与△ACB相似.

【解析】试题分析：（1）根据勾股定理得出AB=5,要使AD=AB=5，∵动点D每秒5个单位的速度运动，∴t=1；（2）当△DEG与△ACB相似时，要分两种情况讨论，根据相似三角形的性质，列出比例式，求出DE的表达式时，要分AD＜AE和AD＞AE两种情况讨论.

试题解析：

（1）∵∠ACB=90°，AC=3，BC=4， ∴AB==5．

∵AD=5t，CE=3t， ∴当AD=AB时，5t=5，即t=1；

∴AE=AC+CE=3+3t=6，DE=6﹣5=1．

（2）∵EF=BC=4，G是EF的中点， ∴GE=2．

当AD＜AE（即t＜）时，DE=AE﹣AD=3+3t﹣5t=3﹣2t，

若△DEG与△ACB相似，则或 ，

∴或， ∴t=或t=；

当AD＞AE（即t＞）时，DE=AD﹣AE=5t﹣（3+3t）=2t﹣3，

若△DEG与△ACB相似，则或 ， ∴或，

解得t=或t=；

综上所述，当t=或 或 或 时，△DEG与△ACB相似．